RiemannMapper : A Mesh Parameterization Toolkit
Background Mesh parameterization refers to the process to map a 3D triangle mesh onto a planar domain, most mesh parameterization algorithms are based on the theories in differential geometry. A conformal mapping maps a 3D surface onto a 2D planar domain, such that the mapping preserves angles, or equivalently,
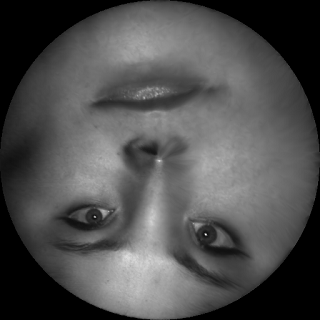
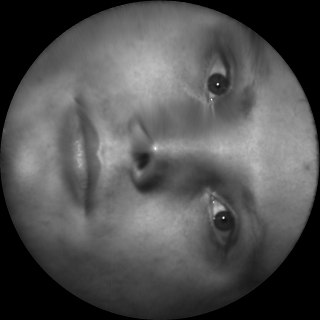
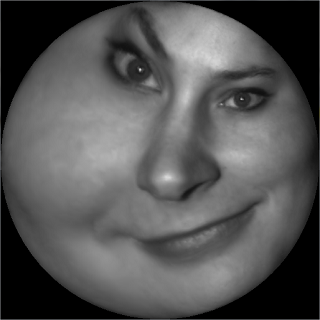
the mapping maps infinitesimal circles on the surface to the infinitesimal circles on the plane. As shown in the following figure, the 3D human face surface is parameterized onto the unit planar
disk by a conformal mapping. We put the checker board texture on the disk, and pull it back onto the 3D face, then all the right corner angles of the checkers are well preserved. Similarly, we put
a circle packing texture on the disk, then pull it back onto the 3D face, then all the small circles are well preserved. According to uniformization theorem, all surfaces in real life can be conformally
mapped to one of 3 canonical shapes, the sphere, the plane and the hyperbolic space. Details can be found in the following books written by the developer of this toolkit.The toolkit demonstrates
the theories and computational algorithms in the books for education and research purposes.
RiemannMapper is a general purpose toolkit for mesh parameterization purpose.
- Written in generic C++ with OpenGL, glut interface
- Developed on both Windows and Linux plat forms
- Handle surfaces with all types of topologies
- Efficient and Robust
The toolkit and the sample mesh files, sample texture images and batch scripts can be downloaded here, the total size is about 83M.
All the computationsa are conducted on discrete surfaces. The smooth surface is sampled and triangualted, we use piecewise Euclidean surface to approximate the original surfaces. Then the triangle mesh is represented using the so-called HalfEdge data structure, the details for HalfEdge data structure can be found here.
If you have any question, please contact David Gu. Your comments and advices will be highly appreciated.
1. Installation Down load the zipped file on a windows platform, unzip the file.The toolkit includes everything you need to execute, it doesn't depend on any other packages or dlls.
2. Input File Format The toolkit supports .obj file and .m file formats. The toolkit package includes many 3D mesh file samples, which are in ASCII text format. You can open them
using text editor and examine. The .m mesh file format is straight forward, it looks like:
Vertex 1 x y z {normal=(nx ny nz) uv=(u v)}
Vertex 2 x y z {normal=(nx ny nz) uv=(u v)}
...
Vertex m x y z {normal=(nx ny nz) uv=(u v)}
Face 1 id1 id2 id3
Face 2 id1 id2 id3
...
Face n id1 id2 id3
where (x,y,z) are the coordinates of a vertex, (nx,ny,nz) are the normal vector on the vertex, (u,v) are the texutre coordinates of the vertex; for each face, (id1,id2,id3) are the vertex ids,
sorted counter-clock-wisely.
3. Hot Keys for viewers
The viewer requires glut32.dll, which can be found at here. After install glut, goto RiemannMapper/Viewer/ directory, double click demo.bat to show the 3D meshes with textures.
The hot keys of the viewers are as follows:
- Left Mouse Button - Pressing the left mouse button and move the mouse, rotate
- Right Mouse Button - Pressing the right mouse button and move the mouse, zoom in an out
- Middle Mouse Button - Pressing the middle mouse button and move the mouse, translate
- Pressing key 't' - toggle texture mapping mode
- Pressing key 'w' - wireframe mode
- Pressing key 's' - smooth shading
- Pressing key 'f' - flat shading
- Pressing key 'Esc' - termination
For MobiusViewer (Mobius.exe)
- Left click in the window to select a pixel, then press 'm' to move the center to the selected pixel
- Press 'r' to rotate the whole disk
Command: RiemannMapper/bin/ViewerConverter.exe sophie.uv.obj sophie.bmp You will see the following demos.
4. Run Demos The toolkit includes many demos to cover surfaces with most possible topologies. You can enter to different subdirectory, inside each directory, there is only one
batch file, named "demo.bat", double click on that script, the demo will be automatically started. In the following, we go through all the demo processes with you. Surfaces are classified
according to their topologies, which are indicated by the number of handles (the called genus) and the number of boundary components. The toolkit parameterizes surfaces with different
topologies with different algorithms. The demo mesh data are organized based on their topologies, each subdirectory contains the sample meshes with the same topology, and the corresponding batch script
to parameterize them. The following list the topological types of demo meshes, click on each item to examine the details:
- Topological Disk - Genus zero surface with a single boundary
- Topological Quadrilaterial - Topological disk with four marked boundary points
- Topological Connected Annulus - Genus zero surface with multiple boundaries
- Topological Sphere - Genus zero surface without any boundary
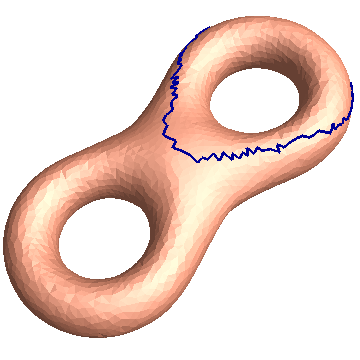
- Topological Torus - Genus one surface without any boundary
- High Genus Surfaces - High genus surface without any boundary
- Topologial Algorithms - Compute cut graph and homology basis
- Remeshing Algorithm - Improve the mesh quality
- Robust Parameterization Algorithm - Parameterize meshes with low qualities
5. Test Using Your Own Mesh You can use the tool kit to parameterize your own data sets.
- Convert your mesh file to either .obj file or .m file
- According to the topology of your mesh file, choose the appropriate subdirectory, copy your mesh there
- Modify the mesh name in the corresponding batch script
- Run the batch script
If you encounter any trouble in testing your own mesh file, please don't hesitate to contact us.
Riemann Mapping
Directory: RiemannMapper/Disk/sophie/
Double Click Demo.bat
Directory: RiemannMapper/Disk/alex/
Double Click Demo.bat
80K vertices and 160K faces.
Mobius Transformation
Conformal Mapping for Topological Sphere
Directory: RiemannMapper/Sphere/bimba/
Double click on Demo.bat
One window pops up, the input mesh is displayed; close this window and wait for the process; another window pops up to show the spherical image.
Extremal Length Using Curvature Flow
Directory: RiemannMapper/Quad/Alex/
Directory: RiemannMapper/Quad/Sophie/
Double Click Demo.bat
Extremal Length using holomorphic differential
Directory: RiemannMapper/Quad2/Alex/
Directory: RiemannMapper/Quad2/Sophie/
Double Click Demo.bat
Directory: RiemannMapper/Annulus/Alex/
Double Click Demo.bat
Circle Domain Mapping
Slit Map
Directory: RiemannMapper/Annulus2/Alex/
Double Click Demo.bat
Directory: RiemannMapper/Torus/Kitten/
Directory: RiemannMapper/Torus/Rocker/
Double Click Demo.bat
Holomorphic Differential
Directory: RiemannMapper/HighGenus/Eight/
Double Click Demo.bat
Hyperbolic Curvature Flow
Directory: RiemannMapper/HighGenus2/Eight/
Double Click Demo.bat
Cut Graph
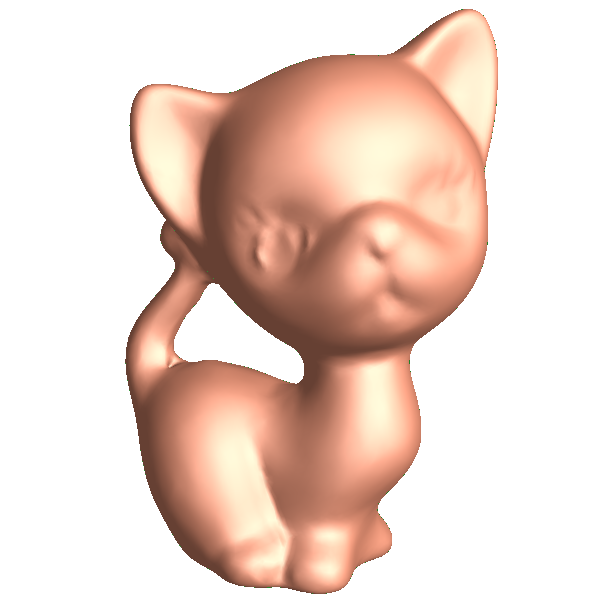
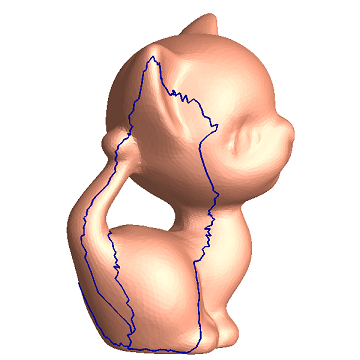
Directory: RiemannMapper/CutGraph/Kitten/
Double Click Demo.bat
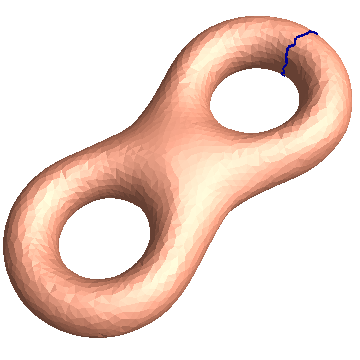
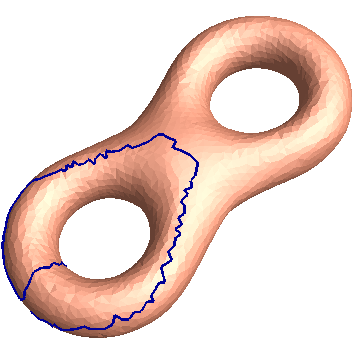
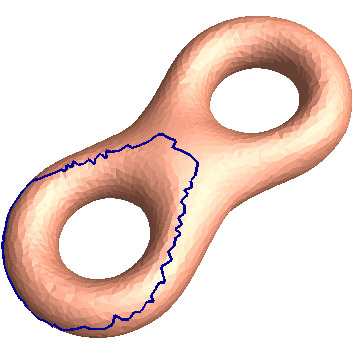
Homology Basis
Directory: RiemannMapper/Homology/Eight/
Double Click Demo.bat
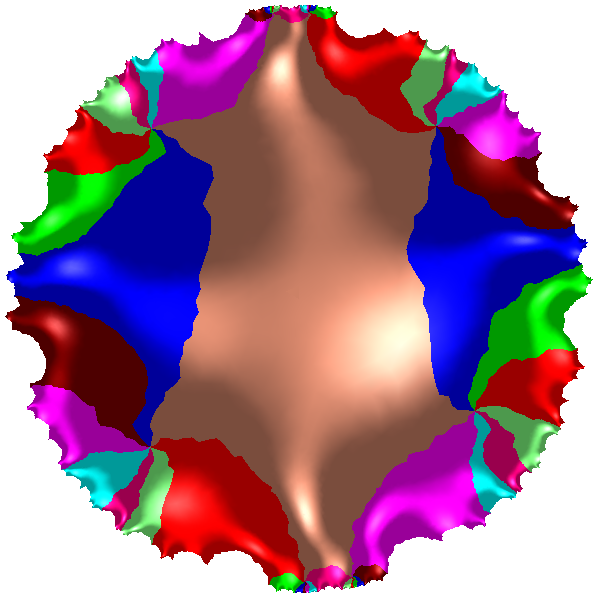
Universal Covering Space
Directory: RiemannMapper/CoveringSpace/Kitten/
Directory: RiemannMapper/CoveringSpace/Eight/
Double Click Demo.bat
|
|
|
Universal Cover of the Kitten
|
Universal Cover of the genus 2 mesh
|
Directory: RiemannMapper/Remesh/Sophie/
Double Click Demo.bat
|
|
|
Input Mesh
|
Remeshed Mesh
|
|
|
|
Input Mesh
|
Remeshed Mesh
|
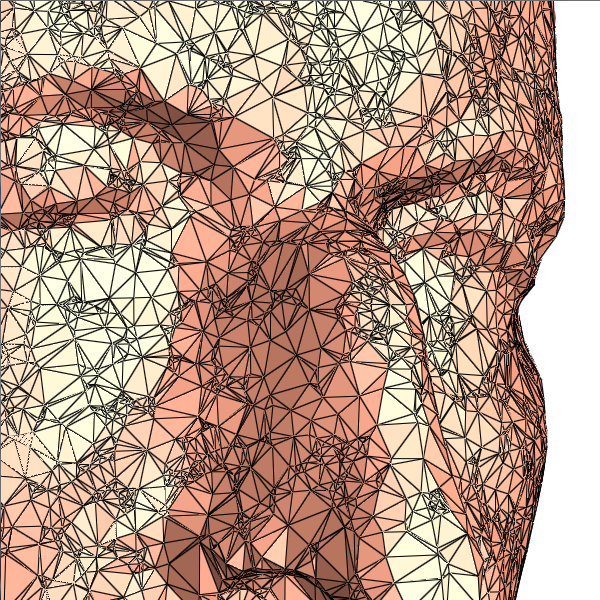
Robust algorithms for meshes with low quality triangulations, such as meshes with too many skinny triangles, or too many obtuse angles.
Directory: RiemannMapper/Robust/MaxPlanck/
Directory: RiemannMapper/Robust/kitten/
Double Click Demo.bat
The RiemannMapper toolkit doesn't include many algorithms invented recently. If you want to get further information about the novel developments, please contact David Gu.