
| Instructor: | David Gu |
| Email: | gu@cs.stonybrook.edu |
| Date: | Every Friday and Saturday 9:00-10:30pm EST |
| Duration: | From July 3rd to September 4th |
| Zoom ID: | 871 6057 8498 |
| Password: | 156302 |
| Live Streaming: | Use a web browser to open the live streaming link online.conformalgeometry.org |
| Host: | Yau Mathematics Science Center of Tsinghua University and Beijing Yanxi Lake Applied Mathematics Institute |
| Participants: | Public to general audience for free |
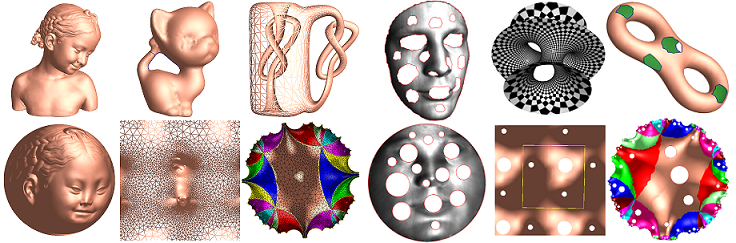
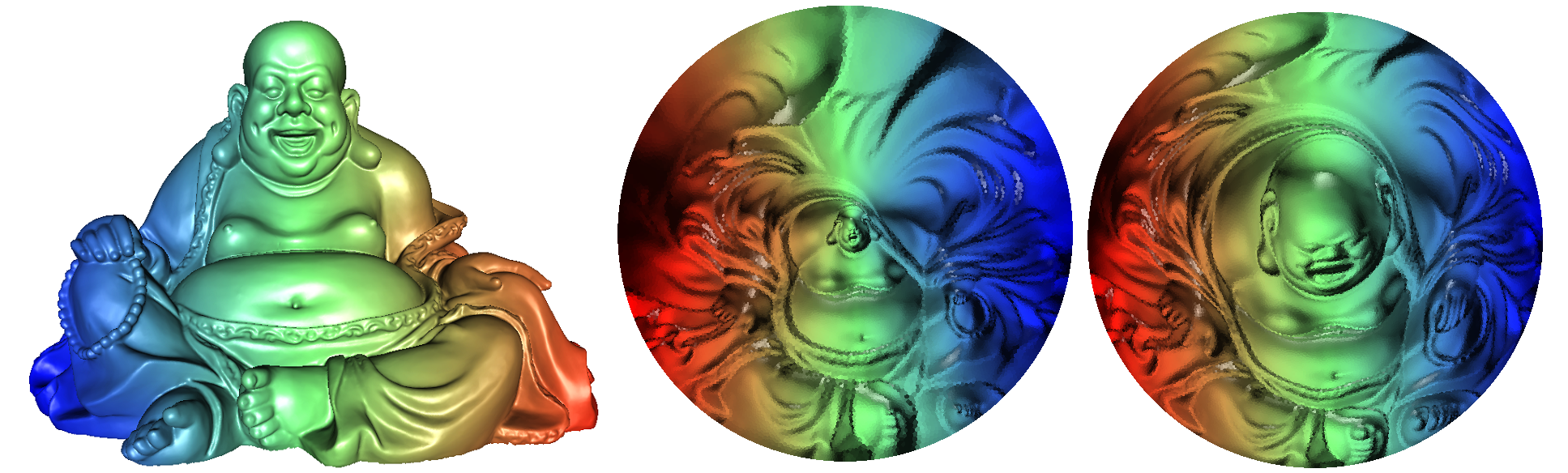
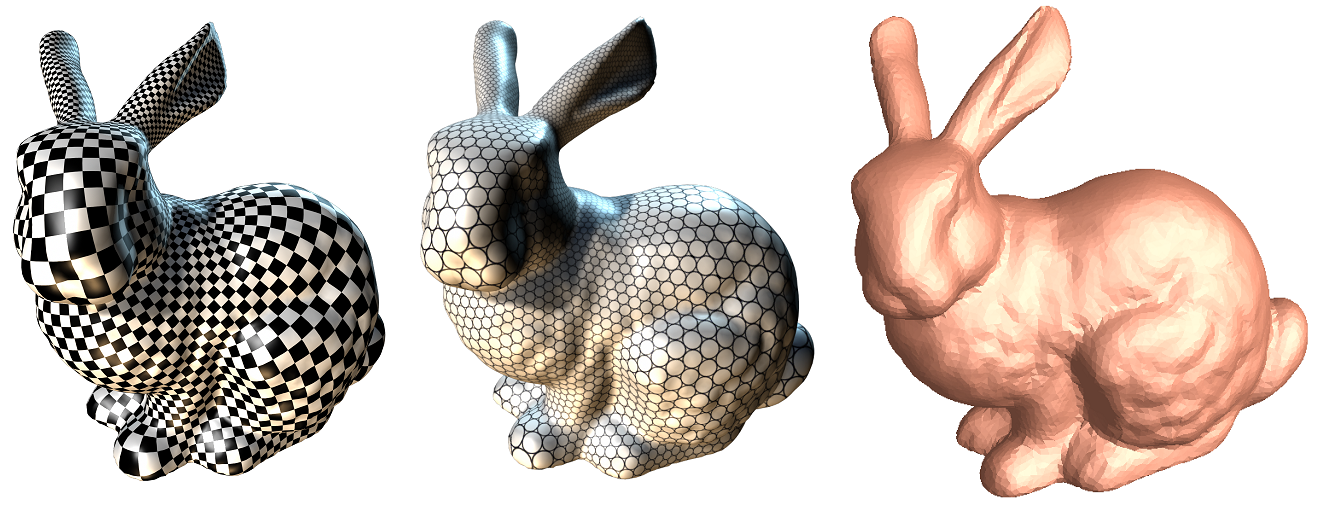
Abstract: This course will cover fundamental concepts and theorems in algebraic topology, surface differential geometry, Riemann surface theory and geometric partial differential equations; it also covers the computational methods for surface fundamental group, homology group, harmonic maps, meromorphic differentials, foliation, conformal mapping, quasi-conformal mapping and Ricci flow. Their applications in Computer Graphics, Computer Vision, Visualization, Geometric Modeling, Networking, Medical Imaging and Deep Learning will be briefly introduced as well.


| No. | Date | Title | Chapter | Download |
| 1. | 07/03/2020 | Introduction to Computational Conformal Geometry | Ch 1 | [pdf] |
| 2. | 07/04/2020 | Algebraic Topology: Fundamental group, Covering space | Ch 2 | [pdf] |
| Assignment 1. | 07/05/2020 | Mesh Halfedge Data Structure and Algorithm for Cut Graph | Ch 2 | [pdf][pdf] |
| 3. | 07/10/2020 | Algebraic Topology: Homology and Cohomology, CW-cell Decomposition | Ch 4, Ch 5 | [pdf] |
| 4. | 07/11/2020 | Fixed point, Poincare-Hopf Index theorem, Characteristic Class of Fiber Bundle | Ch 4, Ch 5 | [pdf] |
| Assignment 2. | 07/16/2020 | Discrete Surface Harmonic Map | Ch 23, Ch 24 | [pdf] |
| 5. | 07/17/2020 | Differential Topology: deRham Cohomology, Hodge Decomposition | Ch 6 | [pdf] |
| 6. | 07/18/2020 | Surface Differential Geometry: fundamental forms, Movable frame method, Gauss-Bonnet theorem | Ch 18 | [pdf] |
| 7. | 07/24/2020 | Isothermal Coordinates and Geodesics | Ch 21, Ch 22, Ch 23 | [pdf] |
| 8. Assignment 3. | 07/25/2020 | Hodge Decomposition and Riemann Mapping | Ch 23, Ch 24 | [pdf] |
| 9. | 07/31/2020 | Harmonic maps and Conformal Maps | Ch 21, Ch 22, Ch 23 | [pdf] |
| 10. | 08/01/2020 | Conformal Module via Geometric Complex Analysis | Ch 8, Ch 9, Ch 10, Ch 11, Ch 13 | [pdf] |
| Assignment 4. | 08/03/2020 | Spherical Harmonic Mapping | Ch 23, Ch 24 | [pdf] |
| 11. | 08/07/2020 | Optimal Transportation : Duality Theorem | Handout | [pdf] |
| 12. | 08/08/2020 | Opitmal Transportation : Convex Geometric View | Handout | [pdf] |
| Assignment 5. | 08/13/2020 | Optimal Transportation Map | Handout | [pdf] |
| 13. | 08/14/2020 | Optimal Transportation: Fluid Dynamics View | Handout | [pdf] |
| 14. | 08/15/2020 | Circle Domain Mapping | Ch 14, Ch 15 | [pdf] |
| Assignment 6. | 08/21/2020 | Circular Slit Map and Koebe's Iteration | Handout | [pdf] |
| 15. | 08/21/2020 | Koebe's Iteration | Ch 14, Ch 15 | [pdf] |
| 16. | 08/22/2020 | Surface Uniformization | Ch 16 | [pdf] |
| 17. | 08/28/2020 | Persistent Homology | Ch 4 | [pdf] |
| 18. | 08/29/2020 | Combinatorial Maps | Ch 25 | [pdf] |
| Assignment 7. | 08/30/2020 | Handle and Tunnel Loops based on persistent homology | Handout | [pdf] |
| 19. | 09/04/2020 | Discrete Surface Ricci Flow | Ch 33, Ch 34 | [pdf] |
| 20. | 09/05/2020 | Generalized Discrete Surface Ricci Flow | Ch 33, Ch 34 | [pdf] |
| 21. | 09/11/2020 | Hyperbolic Geometry | Ch 30, Ch 31 | [pdf] |
| 22. | 09/12/2020 | Uniqueness, existence of the solution to discrete Yamabe flow | Ch 35 | [pdf] |
| Assignment 8. | 09/12/2020 | Surface Hyperbolic Structure | Handout | [pdf][Data Set] |
| 23 | 09/18/2020 | Summary of Computational Conformal Geometry | Handout | [pdf] |
| 24. | 09/26/2020 | Guest Lecture: Dr. Hang Si, Delaunay Triangulations in the Plane | Handout | [pdf] [Demo] |
| 25. | 09/27/2020 | Guest Lecture: Dr. Hang Si, Triangular Mesh Generation in the Plane | Handout | [pdf] |
| Assignment One. | 10/20/2020 | Incremental Algorithm for Convex Hull | Handout | [pdf] |
| 26. | 10/24/2020 | Guest Lecture: Prof. Xiaoming Du, Teichmuller Space | Handout | [pdf] |
| 27. | 10/25/2020 | Guest Lecture: Prof. Xiaoming Du, Mapping Class Group | Handout | [pdf] |
| Assignment Two. | 10/27/2020 | Delaunay Triangulation and Voronoi Diagram | Handout | [pdf] |
| Assignment Three. | 11/06/2020 | Geometric Variational Algorithm for Optimal Transportation Map | Handout | [pdf][data set][bindary demo] |
| Assignment Four. | 11/20/2020 | Geometric Variational Algorithm for Spherical Optimal Transportation Map | Handout | [pdf][data set][bindary demo] |
| 28. | 11/28/2020 | Guest Lecture:Dr. Fei Sun, Algebraic curves, Applications of Riemann-Roch Theory | Handout | [pdf] [pdf] |
| 29. | 11/29/2020 | Guest Lecture:Dr. Fei Sun, Sheaf Cohomology | Handout | [pdf] [pdf] |
| 30. | 12/20/2020 | Guest Lecture:Dr. Xiaoming Du, The hyperbolic structure of the figure-eight knot complement and history of the geometrization theorem for 3-manifolds | Handout | [pdf] |
| Assignment Five. | 12/25/2020 | Incremental Algorithm for 4D Convex Hull | Handout | [pdf] |
| Assignment Six. | 01/03/2021 | 3D Voronoi Diagram | Handout | [pdf] |
| Riemann Surface, meromrophic functions, holomorphic quadratic differentials, foliations | Ch 25, Ch 26 | |||
| Meromorphic differentials, Abel-Jacobi Theorem, | Ch 25 | |||
| Riemann-Roch Theorem | Ch 25 | |||
| Quasi-conformal map, Beltrami equation | Ch 29 |
This lecture briefly introduces the concept of conformal mapping, uniformization theorem, main types of computational algorithms and direct applications in graphics, vision, geometric modeling, networking, medical imaging and deep learning.

