Lecture Notes for Computational Conformal Geometry (2022)
This course will cover fundamental concepts and theorems in algebraic topology, surface differential geometry, Riemann surface theory and geometric partial differential equations; it also covers the computational methods for surface fundamental group, homology group, harmonic maps, meromorphic differentials, foliation, conformal mapping, quasi-conformal mapping and Ricci flow. Their applications in Computer Graphics, Computer Vision, Visualization, Geometric Modeling, Networking, Medical Imaging and Deep Learning will be briefly introduced as well.
The lecture slides are available online.
Lecture Notes for Computational Conformal Geometry (2020)
This course will cover fundamental concepts and theorems in algebraic topology, surface differential geometry, Riemann surface theory and geometric partial differential equations; it also covers the computational methods for surface fundamental group, homology group, harmonic maps, meromorphic differentials, foliation, conformal mapping, quasi-conformal mapping and Ricci flow. Their applications in Computer Graphics, Computer Vision, Visualization, Geometric Modeling, Networking, Medical Imaging and Deep Learning will be briefly introduced as well.
The lecture slides are available online.
Lecture Notes for Computational Conformal Geometry (2019)
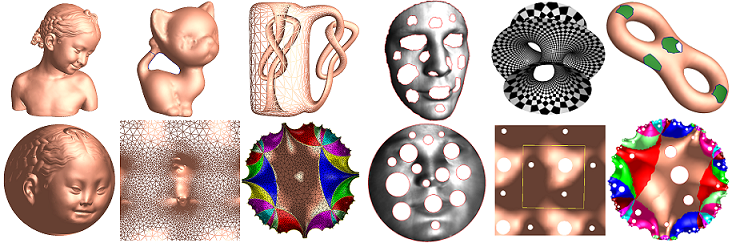This course focuses on the fundamental theories and computational algorithms for conformal geometry. The profound theorems, such as Gauss-Bonnet, Hodge decomposition,
surface Ricci flow, Uniformization were proven in the discrete setting. The major concepts, such as homology/cohomology, fundamental group, holomorphic differential forms,
constant curvature metrics, canonical conformal representations, conformal modules, were calculated using computational algorithms, and visualized by modern graphics techniques.
The course aims at using computational approach and visualization techniques to teach abstract geometric theories.
The lecture slides are available online.
Lecture Notes for Optimal Transportation (2019-2020)
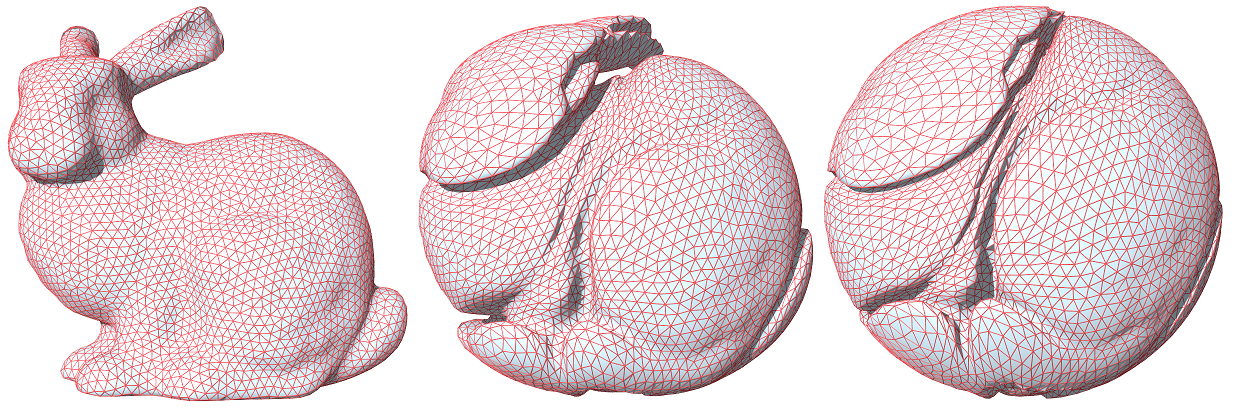
This course focuses on the fundamental theories and computational algorithms for optimal transportation, Monge-Ampere equation and convex geometry.
The topics include Monge-Kantorovich prime, dual problem, Brenier theory; Monge-Ampere equation theory, including existence, uniqueness,
regularity and stability; Alelxandrov convex geometry, Brunn-Minkowski inequality, Alexandrov mapping lemma, Minkowski problem; computational
algorithms, including direct numerical methods for solving Monge-Ampere equation, Oliker-Prussner algorithm, variational method; applications, including
parameterization in graphics, registration in vision, shape comparision in medical imaging and generative models in deep learning.
The lecture notes are available upon request.