Instructor:	David Gu
Email:	gu@cs.stonybrook.edu
Date:	Every Lecture 8:30-10:00am EST
Duration:	Start From July 4th
Voov Meeting ID:	933 8415 7259
Live Streaming:	Use a web browser to open the live streaming link online.conformalgeometry.org
Participants:	Public to general audience

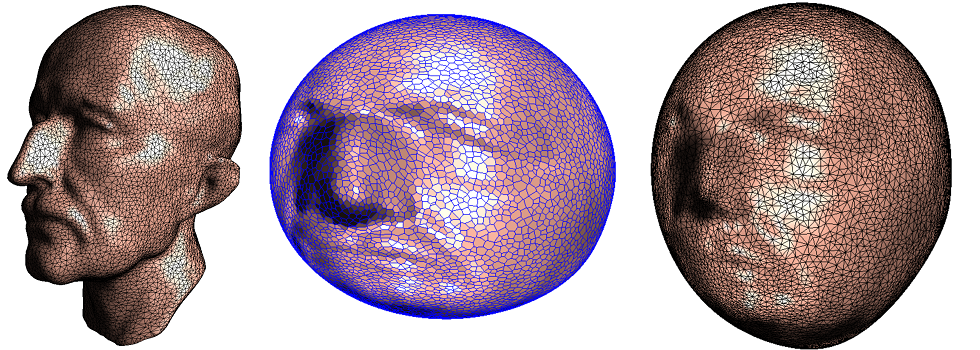
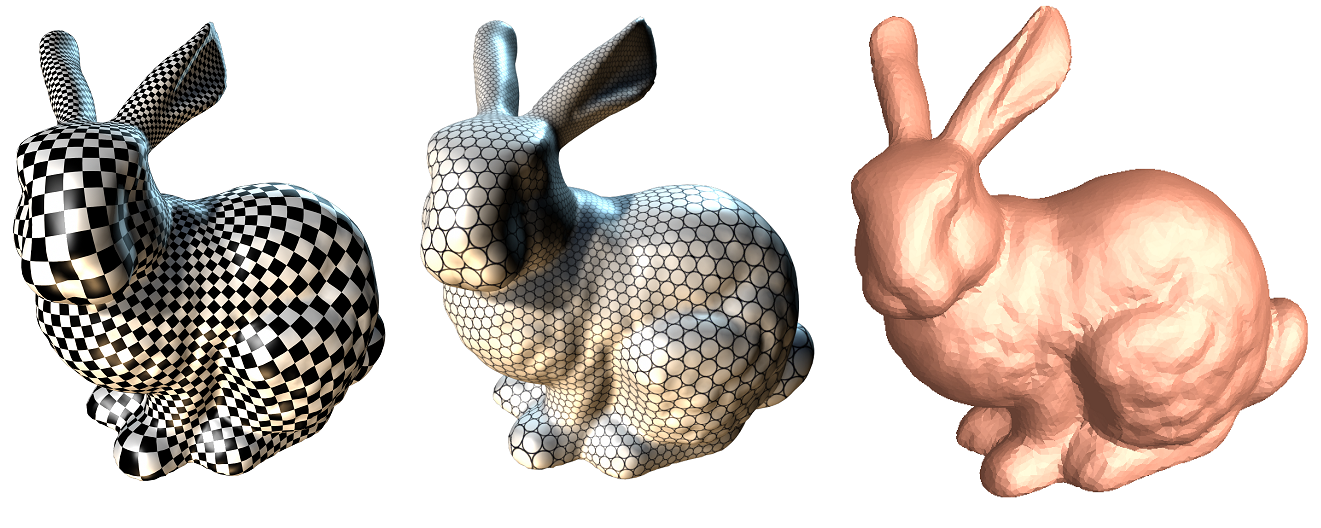
Abstract: This course will cover fundamental concepts and theorems in algebraic topology, surface differential geometry, Riemann surface theory and geometric partial differential equations, as well as optimal transportation theory; it also covers the computational methods for surface fundamental group, homology group, harmonic maps, meromorphic differentials, foliation, conformal mapping, quasi-conformal mapping and Ricci flow. Their applications in Computer Graphics, Computer Vision, Visualization, Geometric Modeling, Networking, Medical Imaging and Deep Learning will be briefly introduced as well.

• Computational Conformal Geometry by Gu and Yau, High Education Press and International Press, 2007.
• Computational Conformal Geometry - Theory by Gu and Yau, High Education Press and International Press, 2020.
• Optimal Transportation - Theory and Computation by Lei and Gu, High Education Press, 2021.

• Classical and Discrete Differential Geometry, Theory, Applications and Algorithmsby Gu and Saucan, CRC Press, 2022
• Ricci Flow for Shape Analysis and Surface Registration - Theories, Algorithms and Applications by Zeng and Gu, Springer 2013.
• Conformal Geometry - Computational Algorithms and Engineering Applicationsby Jin, Gu, He and Wang, Springer 2018.
• Variational Principles for Discrete Surfaces by Luo, Gu and Dai, High Education Press and International Press, 2007.

Lecture Slides

No.	Date	Title	Download
Week One		Algebraic Topology
1.	07/04/2022	Introduction to Computational Conformal Geometry	[pdf]
2.	07/05/2022	Optimal Transportatiton Theory in AI	[pdf]
3.	07/06/2022	Algebraic Topology: Fundamental group, Covering space	[pdf]
4.	07/07/2022	Algebraic Topology: Simplicial Homology and Cohomology	[pdf]
Assignment 1.	07/15/2022	Algorithm Implementation for Fundamental Group	[Data Structure] [Algorithm] [Skeleton Code] [Demo]
		Theoretic Proof for Homology Group	[Problem Set]
Week Two		Differential Topology
5.	07/11/2022	Geometric Programming : Halfedge Data Structure and Algorithmic Design Principle	[Data Structure][Algorithm][demo]
6.	07/12/2022	Fixed point, Poincare-Hopf Index theorem, Characteristic Class of Fiber Bundle	[pdf]
7.	07/13/2022	deRham Cohomology, Hodge Decomposition	[pdf]
8.	07/15/2022	Surface Immersion Regular Homotopy	[pdf]
Assignment 2.	07/22/2022	Algorithm Implementation for Hodge Decomposition	[Algorithm] [Skeleton Code] [Demo]
		Theoretic Proofs for Differential Topology	[Problem Set]
Week Three		Riemannian Metric Structure
9.	07/18/2022	Geometric Programming : Hodge Decomposition	[Algorithm] [demo]
10.	07/19/2022	Surface Differential Geometry, Movable Frame Method	[pdf]
11.	07/20/2022	Yamabe Equation and Geodesics	[pdf]
12.	07/21/2022	Surface Harmonic Maps	[pdf]
Assignment 3.	07/22/2022	Algorithm Implementation for Hodge Decomposition	[Algorithm] [Skeleton Code] [Demo]
		Theoretic Proofs for Surface Differential Geometry	[Problem Set]
Week Four		Conformal Structure
13.	07/25/2022	Conformal Modules via Geometric Complex Analysis	[pdf]
14.	07/26/2022	Circle Domain Mapping: Koebe's Theorem'	[pdf]
15.	07/27/2022	Convergence Analysis of Koebei's Iteration	[pdf]
16.	07/28/2022	Surface Uniformization	[pdf]
Assignment 4.	07/29/2022	Algorithm Implementation for Koebe Iteration	[Algorithm] [Skeleton Code] [Demo]
		Theoretic Proofs for Conformal Structure	[Problem Set]
Week Five		3D Vision
17.	08/01/2022	3D Acquisition Algorithmic Pipeline	[pdf]
18.	08/02/2022	Phase Shifting Structured Light Method	[pdf]
19.	08/03/2022	Camera Calibration, Point Cloud Fusion and Surface Reconstruction	[pdf]
Assignment 5.	08/05/2022	Algorithm Implementation for Stereo-matching using Phase Shifting Structured Light	[Algorithm] [Skeleton Code] [Demo]
Week Six		Persistent Homology
20.	08/08/2022	Persistent Homology	[pdf]
21.	08/09/2022	Combinatorial Map	[pdf]
22.	08/10/2022	Abelian Differential	[pdf]
Assignment 6.	08/12/2022	Handle and Tunnel Loops based on persistent homology	[Algorithm] [Skeleton Code] [Demo]
Week Seven		Riemann Surface Theory
23.	08/15/2022	Abel Differential and Mesh Generation	[pdf]
24.	08/16/2022	Abel-Jacobi Theory	[pdf]
25.	08/17/2022	Riemann-Roch Theory	[pdf]
26.	08/18/2022	Algebraic Function Field on Riemann Surfaces	[pdf]
Assignment 7.	08/22/2022	Verification of Abel-Jacobi Theorem	[Algorithm] [Data]
Week Eight		Surface Ricci Flow
27.	08/22/2022	Discrete Surface Ricci Flow	[pdf]
28.	08/24/2022	Generalized Discrete Surface Ricci Flow	[pdf]
29.	08/26/2022	Hyperbolic Geometry	[pdf]
30.	08/27/2022	Discrete Dynamic Yamabe flow	[pdf]
Assignment 8.	08/28/2022	Surface Hyperbolic Structure	[Algorithm] [Data]
Week Nine		Optiaml Transportation
31.	08/29/2022	Duality Theory	[pdf]
32.	09/05/2022	Convex Geometric View	[pdf]
33.	09/07/2022	Spherical Optimal Transportation	[pdf]
34.	09/09/2022	Fluid Dynamics View	[pdf]
35.	09/10/2022	Computational Methods	[pdf]
Assignment 9.	09/10/2022	Euclidean Optimal Transportation	[Algorithm] [Skeleton Code] [Demo Video]

This lecture briefly introduces the concept of conformal mapping, uniformization theorem, main types of computational algorithms and direct applications in graphics, vision, geometric modeling, networking, medical imaging and deep learning.