Euclidean Optimal Transportation Map
The buddha surface is conformally mapped to the unit planar disk. The surface area element is push-forwarded to the disk.
The optimal transportation map is from the push-forwarded measure to the lebesgue measure.
The optimal transportation map is the gradient map of the Brenier potential. The inverse map is also optimal, which is the
gradient map of the Legendre dual of the Brenier potential.
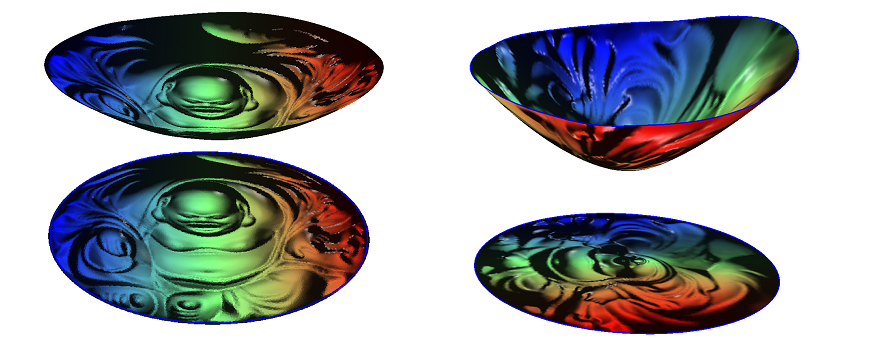
The worst transportation map can be obtained similarly. The middle frame is the
optimal transportation map, the right frame is the wrost transportation map.
Both the optimal transportation map and the worst transportation map are gradient maps
of potential functions. The left frame is the potential for the optimal transportation map, the right frame
is the potential for the worst transportation map.
Spherical Optimal Transportation
The maxplanck head surface is conformally mapped to the unit sphere. The surface area element is push-forwarded to the unit sphere.
The optimal transportation map is from the push-forwarded surface area element to the Hausdorff measure of the unit sphere.
The optimal transportation map is the normal map of the potential, the graph of the potential is shown
in the left frame. The inverse map is also optimal, which is the normal map of the Legendre dual of the potential.
The generalized Legendre dual is shown in the right frame.
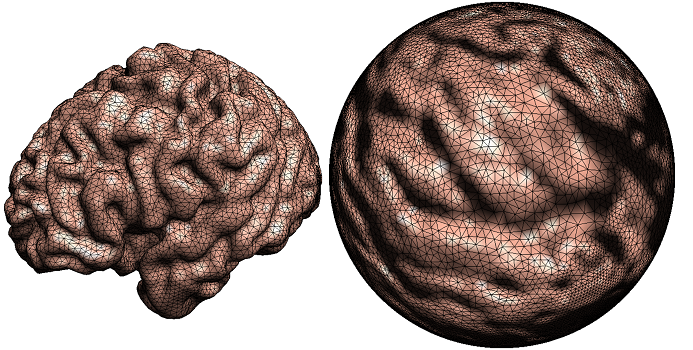
The brain cortical surface is conformally mapped to the unit sphere. The surface area element
is push-forwarded to the unit sphere.
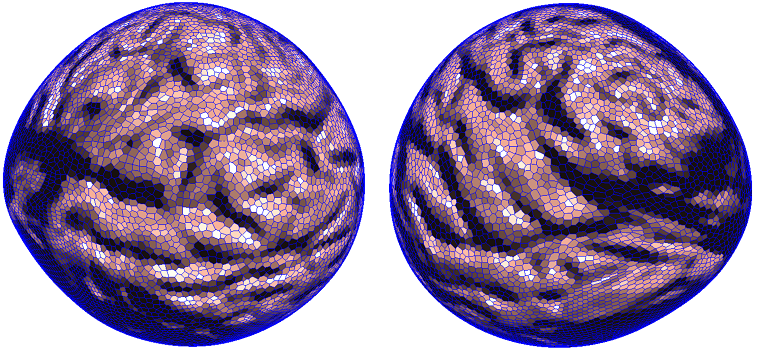
The polar graph of the potential function viewed from different angles.
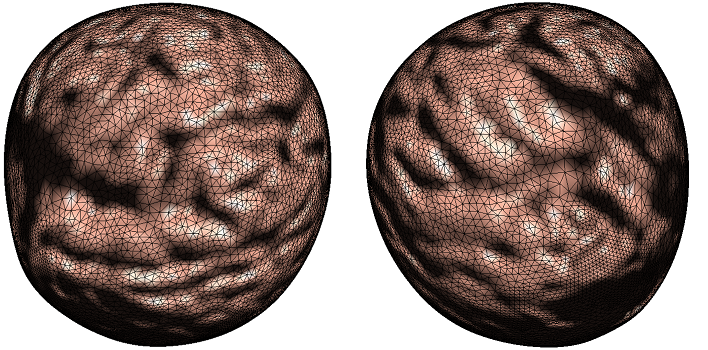
The generalized Legendre dual of the potential function viewed from different angles.
Volumetric Optimal Transportation Map
The volumetric david head model is mapped onto the unit cube by a volumetric harmonic map.
The harmonic map push-forwards the volume element of the david head to the unit cube. The optimal transportation map
is constructed from the push-forwarded volumetric element to the Lebesgue measure.
The volumetric Stanford bunny model is mapped onto the unit ball by a volumetric harmonic map.
The harmonic map push-forwards the volume element of the Stanford bunny to the unit ball. The optimal transportation map
is constructed from the push-forwarded volumetric element to the Lebesgue measure.