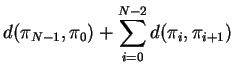Next: TSP's Cost
Up: User and System Manual
Previous: Combinatorial Optimization with DISCROPT
We will go through the process of using DISCROPT to optimize the
Traveling Saleperson problem (TSP): Given  cities find a shortest
tour that visits all
vertices, each exactly once. Each instance of this problem can be
abstractly represented as a weighted complete graph of
cities find a shortest
tour that visits all
vertices, each exactly once. Each instance of this problem can be
abstractly represented as a weighted complete graph of  vertices.
The weight of edge
vertices.
The weight of edge 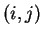 is the distance between city
is the distance between city 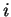 and
and 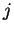 .
A solution, i.e a tour, can be abstractly represented as a circular
permutation of
.
A solution, i.e a tour, can be abstractly represented as a circular
permutation of  numbers. For example, the circular permutation
numbers. For example, the circular permutation
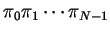 represents the tour starting from city
represents the tour starting from city
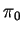 , to
, to 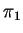 ,
, 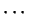 , to
, to 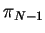 , then coming back to
, then coming back to
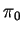 . Then the subjective cost of this solution is:
. Then the subjective cost of this solution is:
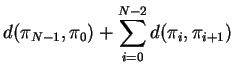
To use DISCROPT, these following functions must be defined:
- double ObjectiveFunction::cost(CircularPermutation & sol) -
takes a solution of type circular permutation and return the objective
cost of the solution. This function must be defined so that the lower
the cost, the better the solution.
- double ObjectiveFunction::delta_cost(CircularPermutation &
sol, const mutation_element & mut_el) - takes a solution and a
mutation, returns the cost of the change from the solution to
the neighboring solution obtained by mutating ``sol'' using the
mutation ``mut_el''. This function is used by such heuristics as
simulated annealing and hill climb heuristics.
- double ObjectiveFunction::extend_cost(CircularPermutation &
sol, const mutation_element & mut_el) - takes a partial
solution and a mutation, returns the cost of the extension from the
solution to the extended neighbor obtained by extending ``sol'' using
the mutation ``mut_el''. This is used by the greedy heuristic.
- double ObjectiveFunction::correctness(CircularPermutation & sol) -
computes the degree of correctness or feasibility of the given solution.
The correctness of a correct solution is 0; a lower number means the
solution is more correct.
- double ObjectiveFunction::delta_correctness(CircularPermutation &
sol, const mutation_element & mut_el) - is similar to
delta_cost. It is used by simulated annealing and hill climb heuristics.
- double ObjectiveFunction::extend_correctness(CircularPermutation &
sol, const mutation_element & mut_el) - is similar to extend_cost.
It is used by the greedy heuristic.
- double ObjectiveFunction::true_cost(CircularPermutation &
sol) - measures the ``real'' objective cost of a
solution. Often, as in TSP, it is the same as cost, but for some
problems cost may be different from true cost, and the users may want
to trace the values of both during search. DISCROPT, however, tries
to find the lowest solution with respect to cost, not true_cost.
- double
ObjectiveFunction::true_correctness(CircularPermutation & sol) -
measures the ``real'' correctness of a solution; similarly defined as
true_cost.
Subsections



Next: TSP's Cost
Up: User and System Manual
Previous: Combinatorial Optimization with DISCROPT
Vinhthuy Phan
2003-05-15
![]() cities find a shortest
tour that visits all
vertices, each exactly once. Each instance of this problem can be
abstractly represented as a weighted complete graph of
cities find a shortest
tour that visits all
vertices, each exactly once. Each instance of this problem can be
abstractly represented as a weighted complete graph of ![]() vertices.
The weight of edge
vertices.
The weight of edge ![]() is the distance between city
is the distance between city ![]() and
and ![]() .
A solution, i.e a tour, can be abstractly represented as a circular
permutation of
.
A solution, i.e a tour, can be abstractly represented as a circular
permutation of ![]() numbers. For example, the circular permutation
numbers. For example, the circular permutation
![]() represents the tour starting from city
represents the tour starting from city
![]() , to
, to ![]() ,
, ![]() , to
, to ![]() , then coming back to
, then coming back to
![]() . Then the subjective cost of this solution is:
. Then the subjective cost of this solution is: