projects people publications datasets

Topology Cuts for Image Segmentation

[publications]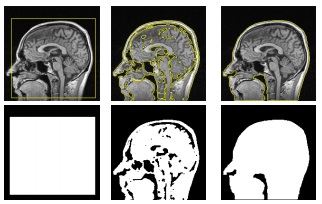

Topology is an important prior in many image segmentation tasks. In this paper, we design and implement a novel graph-based min-cut/max-flow algorithm that incorporates topology priors as global constraints. We show that optimization of the energy function we consider here is NP- hard. However, our algorithm is guaranteed to find an approximate solution that conforms to the initialization, which is a desirable property in many applications since the global optimum solution does not consider any initialization in- formation. The key innovation of our algorithm is the organization of the search for maximum flow in a way that allows consideration of topology constraints. In order to achieve this, we introduce a label attribute for each node to explicitly handle the topology constraints, and we use a distance map to keep track of those nodes that are closest to the boundary. We employ the bucket priority queue data structure that records nodes of equal distance and we efficiently extract the node with minimal distance value. Our methodology of embedding distance functions in a graph- based algorithm is general and can also account for other geometric priors. Experimental results show that our algorithm can efficiently handle segmentation cases that are challenging for graph cuts algorithms. Furthermore, our algorithm is a natural choice for problems with rich topology priors such as object tracking.

Publications
Software