George Hart
Using Great Stella to Join Polyhedral Blocks
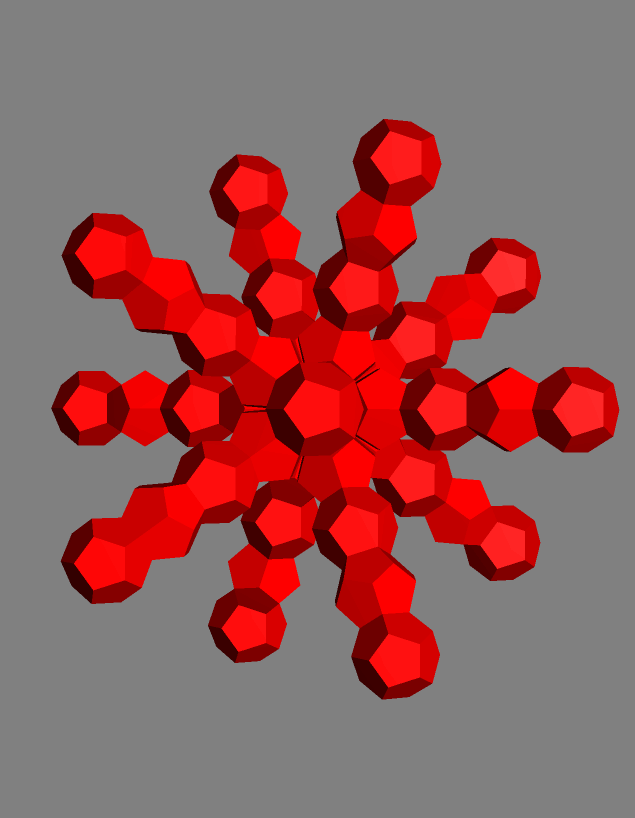
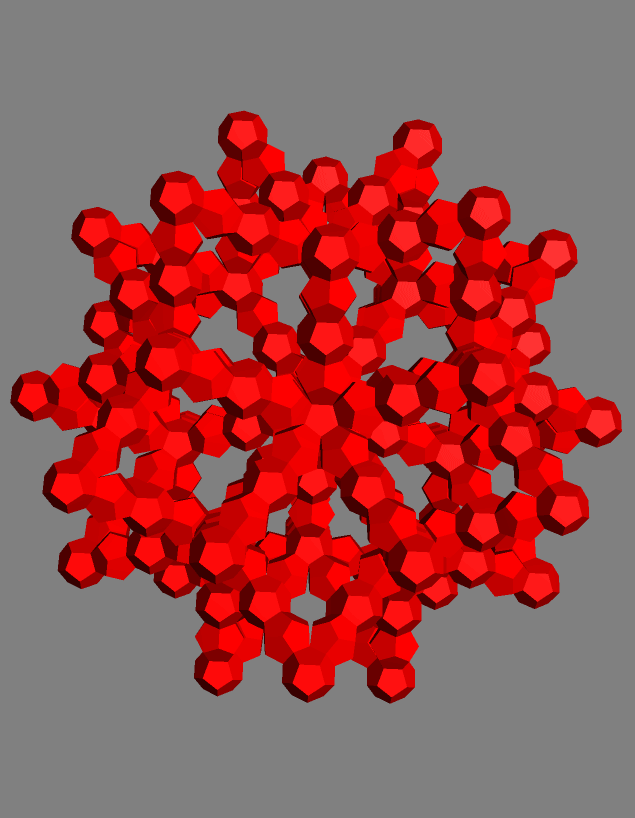
As seen in class, the Great Stella program has a large library of polyhedra and can do various kinds of manipulations on them. For this exercise, we start with simple polyhedra and join them face-to-face to make larger forms. The faces can be unfolded into a net and printed out to be assembled from paper (or plates of steel or whatever).
See the Help file for basic manipulations. For this exercise, you need to understand platonic polyhedra, selecting faces, storing polyhedra in memories, the Augment operation, mirror image reflection, and nonuniform scaling. Be sure you understand how the Augment operation matches the selected faces and that you can rotate with the arrow keys before accepting it. We discovered that the program sometimes crashes if you do these exercises with more than one sub-window open, so type Ctrl-1, which will close all but one sub-window. That is the digit 1. Later you can do Ctrl-2 or Ctrl-3 to reopen 2 or 3 sub-windows.