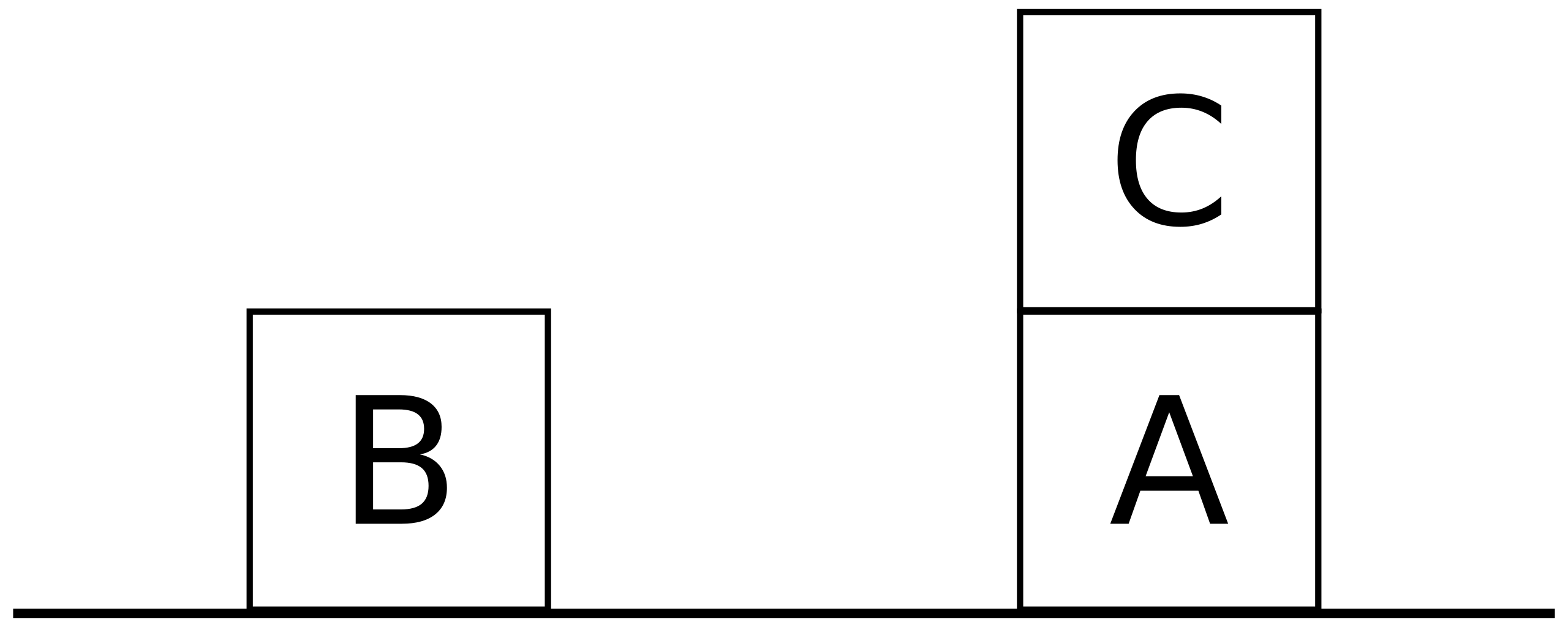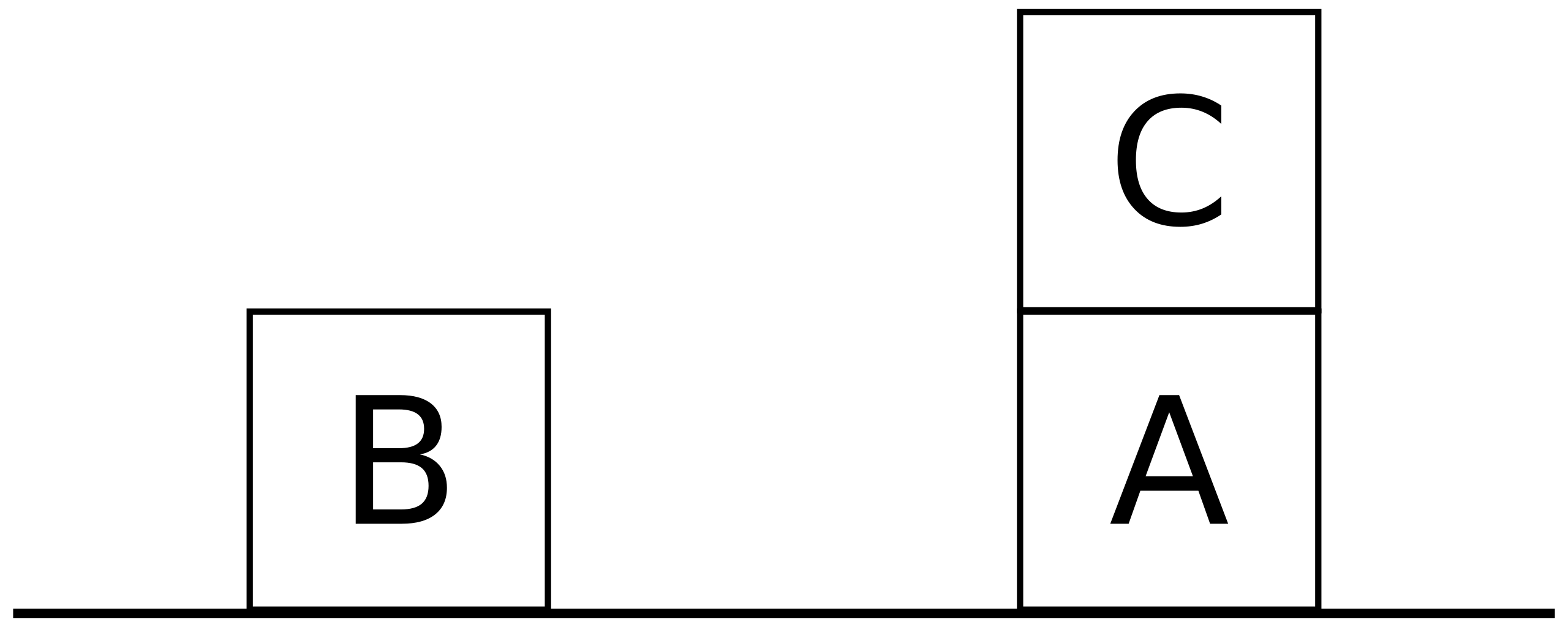CSE 505: Computing with Logic

Part I: Preparation

1. Readable form: Propositions in this form are Prolog atoms (e.g. p1, temp, x, etc.). Formulae, represented by φ can be
   • Propositions
   • Constructed from other formulas using unary connective "\+" (negation) and binary connectives "," (conjunction), ";" (disjunction), "=>" (implication) and "<=>" (equivalence).
   We use the connecties in the usual infix form, using parenthesis to group operations, and, in the absence of parantheses, following the standard convention that the negation operator has the highest precedence, the binary operators are all left associative, with conjunction having higher precedence over implication and equivalence, which, in turn have higher precedence over disjunction.

   All the above syntactic criteria can be easily satisfied by representing the formulae as Prolog terms, and by using the following declaration to specify the precedence and associativity of the implication/equivalence operators : :- op(1050, xfy, (=>)).
:- op(1050, xfy, (<=>)).


2. CNF form: In this form, we use the same propositions as the Readable form, but each formula is
   1. A list of clauses, where
   2. A list of literals, where
   3. Each literal is a proposition, or negation of a proposition (e.g. \+ p)
   Semantically, each clause represents a disjunction of its literals, and each formula is a conjunction of its clauses.

3. Simplified DIMACS form: Most SAT solvers use this format for formulae, specified as a text file. In this form, the propositions are numbered from 1..M. Positive literals are represented by that proposition's number, while negative literals are represented by the corresponding negative number. Formulas are written in CNF using a special notation, as explained below.

   The first line of the file has:

   p  cnf  M  N

   ("p" and "cnf" have to appear as is.) Here, "M" is an integer representing the number of distinct propositions in the formula, and "N" as an integer representing the number of clauses in the formula.

   The remaining lines of the file represent clauses of the formula, each clause appearing in a single line. The literals in the clause are listed on that line (separated by a space). End of clause is marked by "0" (note that "0" does not represent a proposition). The entire file is taken as a formula in conjunctive normal form.

   For instance, the formula in readable form as (q => r), (r,s => q) may be represented as

   p cnf 3 2
-1 2 0
-2 -3 1 0

   (Here q,r,s are propositions 1,2,3 respectively).

Part I: Questions

1. Binary predicate toCNF that, given a formula in Readable form as the first argument, returns its equivalent CNF in the second argument.

   For example, toCNF( ((q => r), (r,s => q)), Q) may return Q=[[\+ q, r], [\+ r, \+ s, q]] (order of literals in clauses, or order of clauses in formula may differ).

   Assume the first argument is in valid readable form, no need to take any special measures to check it.

2. 4-ary predicate toDimacs that, given a formula in CNF form as its first argument, returns its equivalent Dimacs form in its remaining three arguments as follows:
   1. The second argument will be the number of distinct propositions in the formula
   2. The third argument will be the number of clauses in the formula, and
   3. The fourth argument will be the clauses themselves.

   For example, toDimacs([[\+ q, r], [\+ r, \+ s, q]], M, N, Cl) will return M=3, N=2, and Cl = [[-1, 2], [-2, -3, 1]]

3. Unary predicate prop2dimacs that takes a single file name, fn, as an argument, such that fn.prop contains a set of propositional formulae in readable form. Each formula in the .prop file will end with a period ("."). prop2dimacs then writes to fn.cnf the equivalent formula in Dimacs form (including the header, trailing 0s in clauses, etc.). The output .cnf file should be in a form that can input to SAT solvers like minisat, picosat, etc.

Part II: Planning as Satisfiability

Background:

STRIPS-Style planning is done in a setting where world states are described as a set of conditions. We can move from one world state to another by taking one of many available actions. At each step only one action is taken. In this style of planning, we consider only deterministic actions: the result of an action takes us to a specific state. The set of all actions is completely specified.

Each action, act, is specified by

• precondition, pre(act): a set of conditions (or their negations) that must hold,
• positive-postcondition, post-add(act): a set of conditions that will hold in the destination state (i.e., enabled by this action; and
• negative-postcondition, post-delete(act): a set of conditions that will not hold in the destination state (i.e. disabled by this action).

• Init: a set of conditions that characterizes the initial state; and
• Goal: a set of conditions that characterize goal states.

The problem then is to find a sequence of actions that will take us from the initial state to a goal state. There are a number of explanatory resources in the Web for STRIPS-Style planning (e.g. on Wikipedia). Instead of repeating those, we'll give a short illustrative example from Blocks World.

Blocks World Example

Blocks world consists of a number of same-sized wooden blocks that can be stacked on top of each other. Each block can be placed directly on a table (which is large enough to hold all the blocks), or on another (unique) block. Each block may have another (unique) block on top of it, or may be clear.

World states can be specified using the following family of conditions:

• on(b₁, b₂): Block b₁ is on block b₂.
• clear(b₁): Block b₁ is clear: has nothing on top.
• on_table(b₁): Block b₁ is directly on the table.

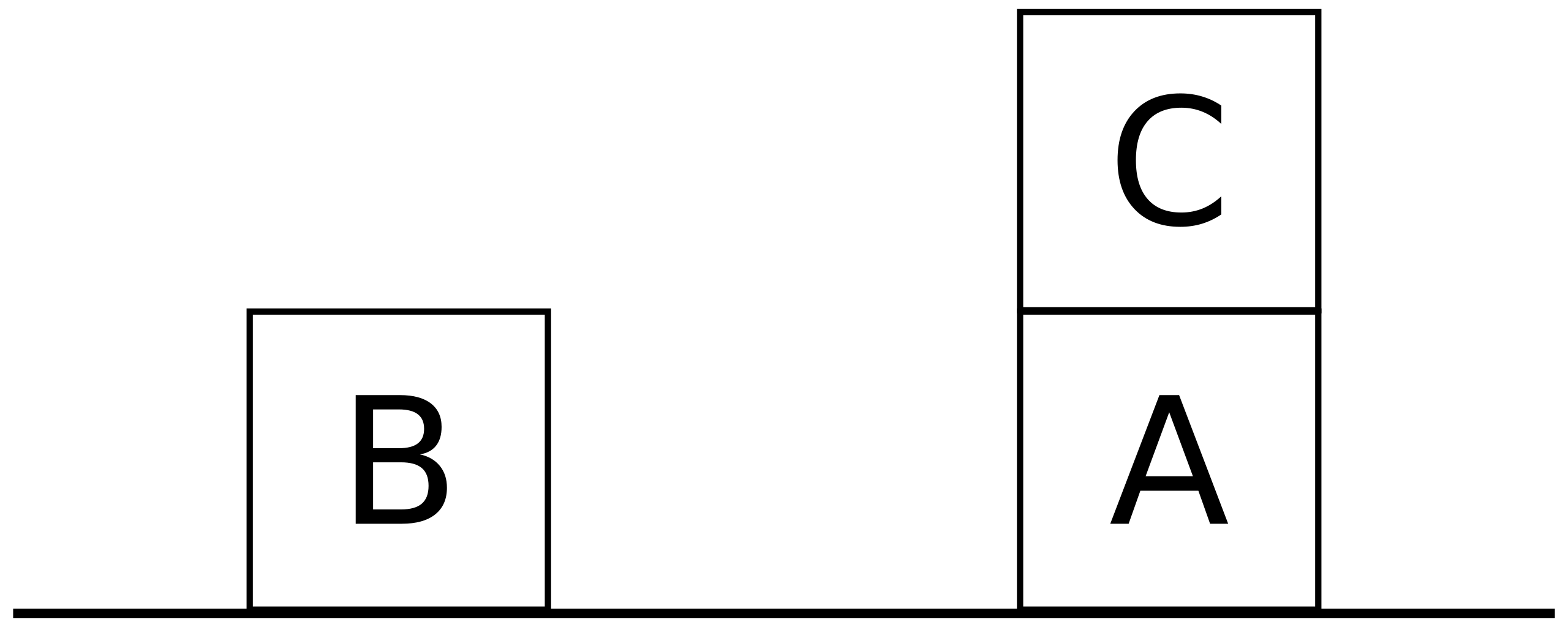
This state can be described by the set of conditions:

on_table(b), on_table(a), on(c, a), clear(b), clear(c)

There are 3 types of actions:

Action	Pre	Post-Add	Post-Del
move_table_to_block(X, Z) Move block X from table to top of block Z:	clear(X), on_table(X), clear(Z)	on(X, Z)	on_table(X), clear(Z)
move_block_to_table(X, Y) Move block X from top of block Y to table:	clear(X), on(X, Y)	on_table(X), clear(Y)	on(X, Y)
move_block_to_block(X, Y, Z) Move block X from top of block Y to top of block Z:	clear(A), on(Z, Y), clear(Z)	on(X, Z), clear(Y)	on(X, Y), clear(Z)

From the state pictured above, we can move block c to top of block b (all preconditions are satisfied). Taking this action will result in state (at Step 2):

on_table(b), on_table(a), on(c, b), clear(a), clear(c)

The only things left to specify for this planning problem are the initial state and the goal states:

For example, the initial state could be

Init = on_table(a), on(b,c), on(c,a), clear(b)

Goal = on(a,c)

Satisfiability:

Note also that the conditions that hold at one state may not hold at a different state. However, the satisfiability problem takes a propositional formula as an input, a formula whose form or meaning does not change over time!

To model the planning problem to satisfiability, we have to invent "static" propositions, which themselves do not change over time, but together capture the dynamic behavior of the planning world's conditions. The key is to embed the "step number".

Important: Since we are given MaxSteps, the "step number" will be between 0 and MaxSteps.

We can introduce two families of propositions:

1. action(Act, i): Action Act was taken at step i.
2. holds(Cond, i): Condition Cond (from the planning problem) holds at step i.

Now, we can map the planning problem to a SAT instance by figuring out how the "holds" and "action" family of propositions are related to each other via the planning problem specification.

State:

A condition C holds at a step I if

• I=0, initial state: if C is in Init
• I>0, a subsequent state: The let A be some action such that action(A, I-1) is true (that is, A was the last action taken). Then, it must be either
  1. C is in post-add(A) (enabled by this action)
  2. C held at step I-1, and C is not in post-del(A)) (i.e., not disabled by this action).

Action:

Say, an action act was taken at step i. Then, clearly, its preconditions must have been true at the previous state. So,

• If action A was chosen at step i, and if P is a precondition of A, then P must hold at i.

Only one action can be taken in any step, so we have

• It is not possible for actions A and B (distinct actions) to be chosen at the same step i.

Part II: Your Task

Planning Instance Description: Each planning instance will be in a separate file, consisting of the following definitions:

• blocks(list). where list is a Prolog list of all the blocks in the instance. For instance, blocks([a,b,c]).
• init(list). where list is a Prolog list of conditions characterizing the initial state of the instance. For instance, init([on(c,b), on(b,a), on_table(a), clear(c)]).
• goal(list). where list is a Prolog list of conditions characterizing the goal states of the instance. For instance, goal([on(a,c), clear(b)]).
• maxstep(n) where n is a positive (non-zero) integer.

Part III: Extra Work, Extra Credit

• There are N locations on the table where blocks can be kept.
• Each location can have at most one block directly on it.
• Each stack of blocks can have at most 2 blocks.
• Each problem instance has at most 2(N-1) blocks.

Write a Prolog program to generate a propositional formula in a Dimacs CNF file, that can then be checked for satisfiability using standard SAT solvers. Again, satisfiability must mean plan existence and vice versa.

Grading:

Submission:

For parts II and III, you can set up private git repositories and share its handle with me. Or send me a zip/tar archive via email.