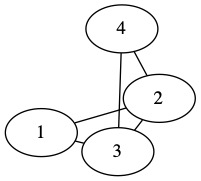
edge(a,1,2).
edge(a,2,3).
edge(a,3,4).
edge(a,1,3).
edge(a,2,4).
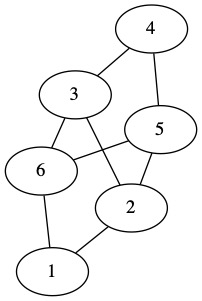
edge(b,1,2).
edge(b,2,3).
edge(b,3,4).
edge(b,4,5).
edge(b,5,6).
edge(b,6,1).
edge(b,2,5).
edge(b,3,6).
For example, pick_odd([1,1,2,3,5,8,13,21,34,55], L) should return L=[1,2,5,13,34].
You may define and use any helper predicates you need.
Answer this question without using arithmetic.
If you use arithmetic you'll get very little credit even if your predicate works as specified.
L2 is a subsequence of L1 if all elements of L2 also occur in L1, and if a occurs before b in L2 then a occurs before b in L1 also.
L is an increasing sequence if the elements are in ascending order: i.e. if a occurs before b in L, then a < b.
For instance, incsub([2,4,1,7,3,8], L2) should succeed with answers L2 = [], L2 = [2], L2 = [4], L2 = [2,4], L2 = [1], ... (upon backtracking; a total of 26 distinct answers).
Each graph is given an identifier (name or number), and we enumerate its edges as triples in a 3-ary edge relation. Each triple of the form edge(i, v1, v2) represents an edge in graph i between vertices v1 and v2. Example graphs and their Prolog encoding are shown below:
| Graph ID | Pictorial Representation | Prolog Representation |
|---|---|---|
| a |

|
|
b |

|
|
For example, for graphs a and b in the above example, three_clique(a) should succeed while three_clique(b) should fail.
For example, simple_path(a, 1, 4, Y) should succeed with Y=[2], and upon backtracking, Y=[3], Y=[2,3], and Y=[3,2]. The order of answers does not matter.
For example, non_bipartite(a) should succeed while non_bipartite(b) should fail.
Code documentation is expected, except where the intent of the solution is obvious from its form. Partial credit may not be possible without clear documentation.
I will post submission instructions shortly.