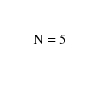About the Book

The Stony Brook Algorithm Repository

Steven Skiena
Stony Brook University
Dept. of Computer Science

• By Language
  • C
  • C++
  • C#
  • Java
  • FORTRAN
  • Python
  • Mathematica
  • Pascal
  • ADA
  • Lisp
  • Binary
• By Problem
  • 1.1 Data Structures
    • Dictionaries
    • Priority Queues
    • Suffix Trees and Arrays
    • Graph Data Structures
    • Set Data Structures
    • Kd-Trees
  • 1.2 Numerical Problems
    • Solving Linear Equations
    • Bandwidth Reduction
    • Matrix Multiplication
    • Determinants and Permanents
    • Constrained and Unconstrained Optimization
    • Linear Programming
    • Random Number Generation
    • Factoring and Primality Testing
    • Arbitrary Precision Arithmetic
    • Knapsack Problem
    • Discrete Fourier Transform
  • 1.3 Combinatorial Problems
    • Sorting
    • Searching
    • Median and Selection
    • Generating Permutations
    • Generating Subsets
    • Generating Partitions
    • Generating Graphs
    • Calendrical Calculations
    • Job Scheduling
    • Satisfiability
  • 1.4 Graph Problems -- polynomial-time problems
    • Connected Components
    • Topological Sorting
    • Minimum Spanning Tree
    • Shortest Path
    • Transitive Closure and Reduction
    • Matching
    • Eulerian Cycle / Chinese Postman
    • Edge and Vertex Connectivity
    • Network Flow
    • Drawing Graphs Nicely
    • Drawing Trees
    • Planarity Detection and Embedding
  • 1.5 Graph Problems -- hard problems
    • Clique
    • Independent Set
    • Vertex Cover
    • Traveling Salesman Problem
    • Hamiltonian Cycle
    • Graph Partition
    • Vertex Coloring
    • Edge Coloring
    • Graph Isomorphism
    • Steiner Tree
    • Feedback Edge/Vertex Set
  • 1.6 Computational Geometry
    • Robust Geometric Primitives
    • Convex Hull
    • Triangulation
    • Voronoi Diagrams
    • Nearest Neighbor Search
    • Range Search
    • Point Location
    • Intersection Detection
    • Bin Packing
    • Medial-Axis Transformation
    • Polygon Partitioning
    • Simplifying Polygons
    • Shape Similarity
    • Motion Planning
    • Maintaining Line Arrangements
    • Minkowski Sum
  • 1.7 Set and String Problems
    • Set Cover
    • Set Packing
    • String Matching
    • Approximate String Matching
    • Text Compression
    • Cryptography
    • Finite State Machine Minimization
    • Longest Common Substring
    • Shortest Common Superstring
• Algorithm Links
  • Algorithm Lectures
  • Algorithm Design Manual Information
  • CSE 373 Course page
  • NIST Dictory of Algorithms and Data Structures
  • World of Mathematics
  • Programming Challenges
  • Graduate Study Opportuinties

The Fast Fourier transform is a DFT algorithm developed by Tukey and Cooley in 1965 which reduces the number of computations from something on the order of N₀² to N₀log N₀. There are basically two types of Tukey-Cooley FFT algorithms in use: decimation-in-time and decimation-in-frequency. The algorithm is simplified if N₀ is chosen to be a power of 2, but it is not a requirement.