1.6.12 Simplifying Polygons
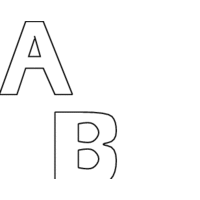
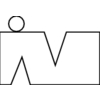
INPUT OUTPUT
Input Description:
A polygon or polyhedron p, with n vertices.
Problem:
Find a polygon or polyhedron p' with n' vertices,
where the shape of p' is close to p while n' << n.
Excerpt from
The Algorithm Design Manual:
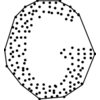
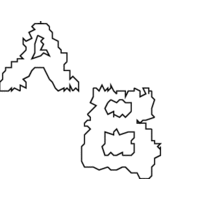
Polygon simplification has two primary applications.
The first is in cleaning up a noisy representation of a polygon,
perhaps obtained by scanning a picture of an object.
By processing it, we hope to remove the noise and reconstruct the
original object.
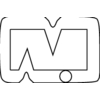
The second is in data compression, where
given a large and complicated
object, we seek to simplify it by reducing detail.
Ideally, we obtain a polygon with far fewer vertices that
looks essentially the same.
This can be a big win in computer graphics, where replacing
a large model with a smaller model might have little visual impact
but be significantly faster to render.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Computational Geometry : Algorithms and Applications
Computational Geometry in C
Discrete Voronoi Skeletons
