Learning to Count

Combinatorics problems are notorious for their reliance on cleverness and insight. Once you look at the problem in the right way, the answer suddenly becomes obvious.

Basic counting techniques include:

• Product Rule - The product rule states that if there are $\vert A\vert$ possibilities from set $A$ and $\vert B\vert$ possibilities from set $B$, then there are $\vert A\vert \times \vert B\vert$ ways to combine one from $A$ and one from $B$.

• Sum Rule - The sum rule states that if there are $\vert A\vert$ possibilities from set $A$ and $\vert B\vert$ possibilities from set $B$, then there are $\vert A\vert + \vert B\vert$ ways for either $A$ or $B$ to occur - assuming the elements of $A$ and $B$ are distinct.

• Inclusion-Exclusion Formula - The sum rule is a special case of a more general formula when the two sets can overlap, namely,
  
  $$\vert A \cup B\vert = \vert A\vert + \vert B\vert - \vert A \cap B\vert$$
  
  
  The reason this works is that summing the sets double counts certain possibilities, namely, those occurring in both sets.

Double counting is a slippery aspect of combinatorics, which can make it difficult to solve problems via inclusion-exclusion.

Combinatorial Objects

A bijection is a one-to-one mapping between the elements of one set and the elements of another. Counting the size of one of the sets automatically gives you the size of the other set.

Exploiting bijections requires us to have a repertoire of sets which we know how to count, so we can map other objects to them.

It is useful to have a feeling for how fast the number of objects grows, to know when exhaustive search breaks down as a possible technique:

• Permutations - A permutation is an arrangement of $n$ items, where every item appears exactly once. There are $n! = \prod_{i=1}^n i$ different permutations. The $3! = 6$ permutations of three items are 123, 132, 213, 231, 312, and 321. For $n=10$, $n! = 3,628,800$.

• Subsets - A subset is a selection of elements from $n$ possible items. There are $2^n$ distinct subsets of $n$ things. Thus there are $2^3 = 8$ subsets of three items, namely, 1, 2, 3, 12, 13, 23, 123, and the empty set: never forget the empty set. For $n=20$, $2^n = 1,048,576$.

• Strings - A string is a sequence of items which are drawn with repetition. There are $m^n$ distinct sequences of $n$ items drawn from $m$ items. There are 27 length-3 strings on 123. The number of binary strings of length $n$ is identical to the number of subsets of $n$ items (why?)

Recurrence Relations

Recurrence relations make it easy to count a variety of recursively defined structures. Recursively defined structures include trees, lists, well-formed formulae, and divide-and-conquer algorithms - so they lurk wherever computer scientists do.

A recurrence relation is an equation which is defined in terms of itself. They are useful because many natural functions are easily expressed as recurrences:

Polynomials:

$$a_{n} = a_{n-1} + 1, a_{1} = 1 \longrightarrow a_{n} = n$$

Exponentials:

$$a_{n} = 2 a_{n-1}, a_{1} = 2 \longrightarrow a_{n} = 2^{n}$$

Weird but interesting functions otherwise hard to represent:

$$a_{n}=n a_{n-1}, a_{1} = 1 \longrightarrow a_{n} = n!$$

It is often easy to find a recurrence as the answer to a counting problem. Solving the recurrence to get a nice closed form can be somewhat of an art, but as we shall see, computer programs can easily evaluate the value of a given recurrence even without the existence of a nice closed form.

Binomial Coefficients

The most important class of counting numbers are the binomial coefficients, where ${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array} \right) }$ counts the number of ways to choose $k$ things out of $n$ possibilities. What do they count?

• Committees - How many ways are there to form a $k$-member committee from $n$ people? By definition, ${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array} \right) }$ is the answer.

• Paths Across a Grid - How many ways are there to travel from the upper-left corner of an $n \times m$ grid to the lower-right corner by walking only down and to the right? Every path must consist of $n+m$ steps, $n$ downward and $m$ to the right. 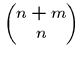Every path with a different set of downward moves is distinct, so there are ${\scriptsize\left( \begin{array}{@{}c@{}} n+m \\ n \end{array} \right) }$ such sets/paths.

• Coefficients of $(a+b)^n$ - Observe that
  
  $$(a+b)^3 = 1 a^3 + 3 a^2 b + 3 a b^2 + 1 b^3$$
  
  
  What is the coefficient of the term $a^k b^{n-k}$? Clearly ${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array} \right) }$, because it counts the number of ways we can choose the $k$ $a$-terms out of $n$ possibilities.

Computing Binomial Coefficients

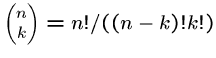Since ${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array} \right) } = n! / ((n-k)! k!)$, in principle you can compute them straight from factorials. However, intermediate calculations can easily cause arithmetic overflow even when the final coefficient fits comfortably within an integer.

A more stable way to compute binomial coefficients is using the recurrence relation implicit in the construction of Pascal's triangle, namely, that

$${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array}... ...e\left( \begin{array}{@{}c@{}} n-1 \\ k \end{array} \right) }$$

Why does this work? Consider whether the $n$th element appears in one of the ${\scriptsize\left( \begin{array}{@{}c@{}} n \\ k \end{array} \right) }$ subsets of $k$ elements. If so, we can complete the subset by picking $k-1$ other items from the other $n-1$. If not, we must pick all $k$ items from the remaining $n-1$. There is no overlap between these cases, and all possibilities are included, so the sum counts all $k$-subsets.

No recurrence is complete without basis cases. How many ways are there to choose 0 things from a set? Exactly one, the empty set. The right term of the sum drives us up to ${\scriptsize\left( \begin{array}{@{}c@{}} k \\ k \end{array} \right) }$. How many ways are there to choose $k$ things from a $k$-element set? Exactly one, the complete set.

Implementation

The following implementation of this recurrence is a good example of programming techniques used in dynamic programming, namely storing a table of results so we can evaluate terms of the recurrence by looking up the appropriate values.

#define MAXN    100             /* largest n or m */

long binomial_coefficient(n,m)
int n,m;                        /* computer n choose m */
{
        int i,j;                /* counters */
        long bc[MAXN][MAXN];    /* table of binomial coefficients */

        for (i=0; i<=n; i++) bc[i][0] = 1;

        for (j=0; j<=n; j++) bc[j][j] = 1;

        for (i=1; i<=n; i++)
                for (j=1; j<i; j++)
                        bc[i][j] = bc[i-1][j-1] + bc[i-1][j];

        return( bc[n][m] );
}

Other Counting Sequences

Several other counting sequences which repeatedly emerge in applications, and which are easily computed using recurrence relations.

• Fibonacci numbers - Defined by the recurrence $F_n = F_{n-1} + F_{n-2}$ and the initial values $F_0 = 0$ and $F_1=1$, they emerge repeatedly because this is perhaps the simplest interesting recurrence relation. The first several values are 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...

• Catalan Numbers - The recurrence and associated closed form
  
  $$C_n = \sum_{k=0}^{n-1} C_k C_{n-1-k} = \frac{1}{n+1} {\scriptsize\left( \begin{array}{@{}c@{}} 2n \\ n \end{array} \right) }$$
  
  
  defines the Catalan numbers, which occur in a surprising number of problems in combinatorics. The first several terms are $2, 5, 14, 42, 132, 429, 1430, \ldots$ when $C_0 = 1$.

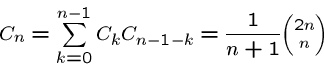
  How many ways are there to build a balanced formula from $n$ sets of left and right parentheses? For example, there are five ways to do it for $n=3$: $((()))$, $()(())$, $(())()$, $(()())$, and $()()()$. The leftmost parenthesis $l$ matches some right parenthesis $r$, which must partition the formula into two balanced pieces, leading to the recurrence.

  The exact same reasoning arises in counting the number of triangulations of a convex polygon, counting the number of rooted binary trees on $n+1$ leaves, and counting the number of paths across a lattice which do not rise above the main diagonal.

• Eulerian Numbers - The Eulerian numbers ${\scriptsize\left\langle \begin{array}{@{}c@{}} n \\ k \end{array} \right\rangle }$ count the number of permutations of length $n$ with exactly $k$ ascending sequences or runs. A recurrence can be formulated by considering each permutation $p$ of $1, ... , n-1$. There are $n$ places to insert element $n$, and each either splits an existing run of $p$ or occurs immediately after the last element of an existing run, thus preserving the run count. Thus ${\scriptsize\left\langle \begin{array}{@{}c@{}} n \\ k \end{array} \right\rang... ...size\left\langle \begin{array}{@{}c@{}} n-1 \\ k-1 \end{array} \right\rangle }$.

• Integer Partitions - An integer partition of $n$ is an unordered set of positive integers which add up to $n$. For example, there are seven partitions of 5, namely, $(5)$, $(4,1)$, $(3,2)$, $(3,1,1)$, $(2,2,1)$, $(2,1,1,1)$, and $(1,1,1,1,1)$. The easiest way to count them is to define a function $f(n,k)$ giving the number of integer partitions of $n$ with largest part at most $k$. In any acceptable partition the largest part either does or does not reach with limit, so $f(n,k) = f(n-k,k) + f(n,k-1)$. The basis cases are $f(1,1) = 1$ and $f(n,k) =0$ whenever $k > n$.

Assigned Problems

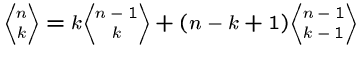110603 (Counting) - How many ways can we express $n$ as the sum of 2s, 3s, and two types of 1?

110604 (Expressions) - How many ways can we build a well-formed formula from $n$ parentheses with nesting depth $d$?

110606 (The Priest Mathematician) - What is the best way to solve a 4-peg Tower of Hanoi puzzle?

110607 (Self-describing Sequence) - What is the $i$th value of the sequence containing $f(k)$ occurrences of $k$ for each $k$, i.e. 1, 2, 2, 3, 3, 4 ,4, 4, 5, 5, 6 ...? What if $i$ is too large to construct the entire sequence in memory?