Graphs
Lecture 27

Steven S. Skiena

Graphs

A graph G consists of a set of vertices V together with a set E of vertex pairs or edges.

Graphs are important because any binary relation is a graph, so graphs can be used to represent essentially any relationship.

Example: A network of roads, with cities as vertices and roads between cities as edges.

Example: An electronic circuit, with junctions as vertices as components as edges.

To understand many problems, we must think of them in terms of graphs!

The Friendship Graph

Consider a graph where the vertices are people, and there is an edge between two people if and only if they are friends.  

This graph is well-defined on any set of people: SUNY SB, New York, or the world.

What questions might we ask about the friendship graph?

• If I am your friend, does that mean you are my friend?

  A graph is undirected if (x,y) implies (y,x). Otherwise the graph is directed. The ``heard-of'' graph is directed since countless famous people have never heard of me! The ``had-sex-with'' graph is presumably undirected, since it requires a partner.

• Am I my own friend?

  An edge of the form (x,x) is said to be a loop. If x is y's friend several times over, that could be modeled using multiedges, multiple edges between the same pair of vertices. A graph is said to be simple if it contains no loops and multiple edges.

• Am I linked by some chain of friends to the President?

  A path is a sequence of edges connecting two vertices. Since Mel Brooks is my father's-sister's-husband's cousin, there is a path between me and him!

• How close is my link to the President?

  If I were trying to impress you with how tight I am with Mel Brooks, I would be much better off saying that Uncle Lenny knows him than to go into the details of how connected I am to Uncle Lenny. Thus we are often interested in the shortest path between two nodes.

• Is there a path of friends between any two people?

  A graph is connected if there is a path between any two vertices. A directed graph is strongly connected if there is a directed path between any two vertices.

• Who has the most friends?

  The degree of a vertex is the number of edges adjacent to it.

• What is the largest clique?

  A social clique is a group of mutual friends who all hang around together. A graph theoretic clique is a complete subgraph, where each vertex pair has an edge between them. Cliques are the densest possible subgraphs. Within the friendship graph, we would expect that large cliques correspond to workplaces, neighborhoods, religious organizations, schools, and the like.

• How long will it take for my gossip to get back to me?

  A cycle is a path where the last vertex is adjacent to the first. A cycle in which no vertex repeats (such as 1-2-3-1 verus 1-2-3-2-1) is said to be simple. The shortest cycle in the graph defines its girth, while a simple cycle which passes through each vertex is said to be a Hamiltonian cycle.

Data Structures for Graphs

There are two main data structures used to represent graphs.

Adjacency MatricesAn adjacency matrix is an matrix, where M[i,j] = 0 iff there is no edge from vertex i to vertex j  

It takes time to test if (i,j) is in a graph represented by an adjacency matrix.

Can we save space if (1) the graph is undirected? (2) if the graph is sparse?

Adjacency ListsAn adjacency list consists of a array of pointers, where the ith element points to a linked list of the edges incident on vertex i.

To test if edge (i,j) is in the graph, we search the ith list for j, which takes , where is the degree of the ith vertex.

Note that can be much less than n when the graph is sparse. If necessary, the two copies of each edge can be linked by a pointer to facilitate deletions.

Tradeoffs Between Adjacency Lists and Adjacency Matrices

Both representations are very useful and have different properties, although adjacency lists are probably better for most problems.

Traversing a Graph

One of the most fundamental graph problems is to traverse every edge and vertex in a graph. Applications include:

• Printing out the contents of each edge and vertex.
• Counting the number of edges.
• Identifying connected components of a graph.

For efficiency, we must make sure we visit each edge at most twice.

For correctness, we must do the traversal in a systematic way so that we don't miss anything.

Since a maze is just a graph, such an algorithm must be powerful enough to enable us to get out of an arbitrary maze.

Marking Vertices

The idea in graph traversal is that we must mark each vertex when we first visit it, and keep track of what have not yet completely explored.

For each vertex, we can maintain two flags:

• discovered - have we ever encountered this vertex before?
• completely-explored - have we finished exploring this vertex yet?

We must also maintain a structure containing all the vertices we have discovered but not yet completely explored.

Initially, only a single start vertex is considered to be discovered.

To completely explore a vertex, we look at each edge going out of it. For each edge which goes to an undiscovered vertex, we mark it discovered and add it to the list of work to do.

Note that regardless of what order we fetch the next vertex to explore, each edge is considered exactly twice, when each of its endpoints are explored.

Correctness of Graph Traversal

Every edge and vertex in the connected component is eventually visited.

Suppose not, ie. there exists a vertex which was unvisited whose neighbor was visited. This neighbor will eventually be explored so we would visit it:

Traversal Orders

The order we explore the vertices depends upon what kind of data structure is used:

• Queue - by storing the vertices in a first-in, first out (FIFO) queue, we explore the oldest unexplored vertices first. Thus our explorations radiate out slowly from the starting vertex, defining a so-called breadth-first search.
• Stack - by storing the vertices in a last-in, first-out (LIFO) stack, we explore the vertices by lurching along a path, constantly visiting a new neighbor if one is available, and backing up only if we are surrounded by previously discovered vertices. Thus our explorations quickly wander away from our starting point, defining a so-called depth-first search.

The three possible colors of each node reflect if it is unvisited (white), visited but unexplored (grey) or completely explored (black).

Breadth-First Search

BFS(G,s)

for each vertex    do

		 color[u] = white

		   , ie. the distance from s

		 p[u] = NIL, ie. the parent in the BFS tree

color[u] = grey

d[s] = 0

p[s] = NIL

  

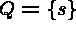
while    do

		 u = head[Q]

		 for each    do

		 		 if color[v] = white then

		 		 		 color[v] = gray

		 		 		 d[v] = d[u] + 1

		 		 		 p[v] = u

		 		 		 enqueue[Q,v]

		 		 dequeue[Q]

		 		 color[u] = black 

Depth-First Search

DFS has a neat recursive implementation which eliminates the need to explicitly use a stack.

Discovery and final times are sometimes a convenience to maintain.

DFS(G)

for each vertex    do

		 color[u] = white

		 parent[u] = nil

time = 0

for each vertex    do

		 if color[u] = white then DFS-VISIT[u]

Initialize each vertex in the main routine, then do a search from each connected component. BFS must also start from a vertex in each component to completely visit the graph.

DFS-VISIT[u]

color[u] = grey (*u had been white/undiscovered*)

discover[u] = time

time = time+1

for each    do

		 if color[v] = white then

		 		 parent[v] = u

		 		 DFS-VISIT(v)

color[u] = black (*now finished with u*)

finish[u] = time

time = time+1

• About this document ...