Steven S. Skiena
Hashing
One way to convert form names to integers is to use the letters to form a base ``alphabet-size'' number system:
To convert ``STEVE'' to a number, observe that e is the 5th letter of the alphabet, s is the 19th letter, t is the 20th letter, and v is the 22nd letter.
Thus ``Steve''
Thus one way we could represent a table of names would be to set aside an array big enough to contain one element for each possible string of letters, then store data in the elements corresponding to real people. By computing this function, it tells us where the person's phone number is immediately!!
What's the Problem?
Because we must leave room for every possible string, this method will use an incredible amount of memory. We need a data structure to represent a sparse table, one where almost all entries will be empty.
We can reduce the number of boxes we need if we are willing to put more than one thing in the same box!
Example: suppose we use the base alphabet number system,
then take the remainder 
Now the table is much smaller, but we need a way to deal with the fact that more than one, (but hopefully every few) keys can get mapped to the same array element.
The Basics of Hashing
The basics of hashing is to apply a function to the search key so we can determine where the item is without looking at the other items. To make the table of reasonable size, we must allow for collisions, two distinct keys mapped to the same location.
There are several clever techniques we will see to develop good hash functions and deal with the problems of duplicates.
Hash Functions
The verb ``hash'' means ``to mix up'', and so we seek a function to mix up keys as well as possible.
The best possible hash function would hash m keys into n ``buckets''
with no more than 
keys per
bucket. Such a function is called a perfect hash function
How can we build a hash function?
Let us consider hashing character strings to integers. The ORD function returns the character code associated with a given character. By using the ``base character size'' number system, we can map each string to an integer.
The First Three SSN digits Hash
The first three digits of the Social Security Number
The last three digits of the Social Security Number
What is the big picture?
Ideas for Hash Functions
Prime Numbers are Good Things
Suppose we wanted to hash check totals by the dollar value in pennies mod 1000. What happens?
,
, and
Prices tend to be clumped by similar last digits, so we get clustering.
If we instead use a prime numbered Modulus like 1007,
these clusters will get broken:
,
, and
.
In general, it is a good idea to use prime modulus for hash table size, since it is less likely the data will be multiples of large primes as opposed to small primes - all multiples of 4 get mapped to even numbers in an even sized hash table!
The Birthday Paradox
No matter how good our hash function is, we had better be prepared for collisions, because of the birthday paradox.
Assuming 365 days a year, what is the probability that exactly two people share a birthday? Once the first person has fixed their birthday, the second person has 365 possible days to be born to avoid a collision, or a 365/365 chance.
With three people, the probability that no two share is 
. In general,
the probability of there being no collisions after n insertions
into an m-element table is
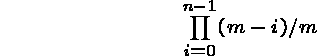
When m = 366, this probability sinks below 1/2 when N = 23 and
to almost 0 when 
.
The moral is that collisions are common, even with good hash functions.
What about Collisions?
No matter how good our hash functions are, we must deal with collisions. What do we do when the spot in the table we need is occupied?
Collision Resolution by Chaining
The easiest approach is to let each element in the hash table be a pointer to a list of keys.
Insertion, deletion, and query reduce to the problem in linked lists. If the n keys are distributed uniformly in a table of size m/n, each operation takes O(m/n) time.
Chaining is easy, but devotes a considerable amount of memory to pointers, which could be used to make the table larger. Still, it is my preferred method.
Open Addressing
We can dispense with all these pointers by using an implicit reference derived from a simple function:
If the space we want to use is filled, we can examine the remaining locations:
The reason for using a more complicated scheme is to avoid long runs from similarly hashed keys.
Deletion in an open addressing scheme is ugly, since removing one element can break a chain of insertions, making some elements inaccessible.
Performance on Set Operations
With either chaining or open addressing:
Pragmatically, a hash table is often the best data structure to maintain a dictionary. However, the worst-case running time is unpredictable.
The best worst-case bounds on a dictionary come from balanced binary trees, such as red-black trees.