Asymptotics
Lecture 15

Steven S. Skiena

Analyzing Algorithms

There are often several different algorithms which correctly solve the same problem. How can we choose among them? There can be several different criteria:

• Ease of implementation
• Ease of understanding
• Efficiency in time and space

The first two are somewhat subjective. However, efficiency is something we can study with mathematical analysis, and gain insight as to which is the fastest algorithm for a given problem.

Time Complexity of Programs

What would we like as the result of the analysis of an algorithm? We might hope for a formula describing exactly how long a program implementing it will run.

Example: Binary search will take milliseconds on an array of n elements.

This would be great, for we could predict exactly how long our program will take. But it is not realistic for several reasons:

1. Dependence on machine type - Obviously, binary search will run faster on a CRAY than a PC. Maybe binary search will now take ms?
2. Dependence on language/compiler - Should our time analysis change when someone uses an optimizing compiler?
3. Dependence of the programmer - Two different people implementing the same algorithm will result in two different programs, each taking slightly differed amounts of time.
4. Should your time analysis be average or worst case? - Many algorithms return answers faster in some cases than others. How did you factor this in? Exactly what do you mean by average case?
5. How big is your problem? - Sometimes small cases must be treated different from big cases, so the same formula won't work.

Time Complexity of Algorithms

For all of these reasons, we cannot hope to analyze the performance of programs precisely. We can analyze the underlying algorithm, but at a less precise level.

Example: Binary search will use about iterations, where each iteration takes time independent of n, to search an array of n elements in the worst case.

Note that this description is true for all binary search programs regardless of language, machine, and programmer.

By describing the worst case instead of the average case, we saved ourselves some nasty analysis. What is the average case?

Algorithms for Multiplications

Everyone knows two different algorithms for multiplication: repeated addition and digit-by-digit multiplication.

Which is better? Let's analyze the complexity of multiplying an n-digit number by an m-digit number, where .

In repeated addition, we explicity use that . Thus adding an n-digit + m-digit number, requires ``about'' n+m steps, one for each digit.

How many additions can we do in the worst case? The biggest n-digit number is all nines, and .

The total time complexity is the cost per addition times the number of additions, so the total complexity .

Digit-by-Digit Multiplication

Since multiplying one digit by one other digit can be done by looking up in a multiplication table (2D array), each step requires a constant amount of work.

Thus to multiply an n-digit number by one digit requires ``about'' n steps. With m ``extra'' zeros (in the worst case), ``about'' n + m steps certainly suffice.

We must do m such multiplications and add them up - each add costs as much as the multiplication.

The total complexity is the cost-per-multiplication * number-of-multiplications + cost-per-addition * number-of- multiplication .

Which is faster?

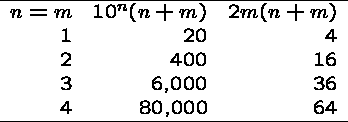
Clearly the repeated addition method is much slower by our analysis, and the difference is going to increase rapidly with n...

Further, it explains the decline and fall of Roman empire - you cannot do digit-by-digit multiplication with Roman numbers!

Growth Rates of Functions

To compare the efficiency of algorithms then, we need a notation to classify numerical functions according to their approximate rate of growth.

We need a way of exactly comparing approximately defined functions. This is the big Oh Notation:

If f(n) and g(n) are functions defined for positive integers, then f(n)= O(g(n)) means that there exists a constant c such that for all sufficiently large positive integers.

The idea is that if f(n)=O(g(n)), then f(n) grows no faster (and possibly slower) than g(n).

Note this definition says nothing about algorithms - it is just a way to compare numerical functions!

Examples

Example: is . Why? For all n > 100, clearly , so it satisfies the definition for c=100.

Example: is not . Why? No matter what value of c you pick, is not true for n>c!

In the big Oh Notation, multiplicative constants and lower order terms are unimportant. Exponents are important.

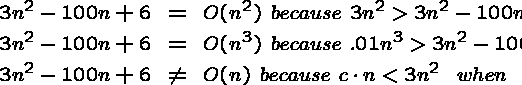
Ranking functions by the Big Oh

The following functions are different according to the big Oh notation, and are ranked in increasing order:

O(1) Constant growth

Logarithmic growth (note:independent of base!)

Polynomial growth: ordered by exponent

O(n) Linear Growth

Quadratic growth

Exponential growth

Why is the big Oh a Big Deal?

Suppose I find two algorithms, one of which does twice as many operations in solving the same problem. I could get the same job done as fast with the slower algorithm if I buy a machine which is twice as fast.

But if my algorithm is faster by a big Oh factor - No matter how much faster you make the machine running the slow algorithm the fast-algorithm, slow machine combination will eventually beat the slow algorithm, fast machine combination.

I can search faster than a supercomputer for a large enough dictionary, If I use binary search and it uses sequential search!

An Application: The Complexity of Songs

Suppose we want to sing a song which lasts for n units of time. Since n can be large, we want to memorize songs which require only a small amount of brain space, i.e. memory.    

Let S(n) be the space complexity of a song which lasts for n units of time.

The amount of space we need to store a song can be measured in either the words or characters needed to memorize it. Note that the number of characters is since every word in a song is at most 34 letters long - Supercalifragilisticexpialidocious!

What bounds can we establish on S(n)? S(n) = O(n), since in the worst case we must explicitly memorize every word we sing - ``The Star-Spangled Banner''

The Refrain

Most popular songs have a refrain, which is a block of text which gets repeated after each stanza in the song:  

Bye, bye Miss American pie
Drove my chevy to the levy but the levy was dry
Them good old boys were drinking whiskey and rye
Singing this will be the day that I die.

Refrains made a song easier to remember, since you memorize it once yet sing it O(n) times. But do they reduce the space complexity?

Not according to the big oh. If

Then the space complexity is still O(n) since it is only halved (if the verse-size = refrain-size):

The k Days of Christmas

To reduce S(n), we must structure the song differently.

Consider ``The k Days of Christmas''. All one must memorize is:

On the kth Day of Christmas, my true love gave to me,

On the First Day of Christmas, my true love gave to me, a partridge in a pear tree

But the time it takes to sing it is

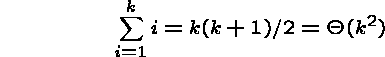
If , then , so . 100 Bottles of Beer

What do kids sing on really long car trips?

n bottles of beer on the wall,
n bottles of beer.
You take one down and pass it around
n-1 bottles of beer on the ball.

All you must remember in this song is this template of size , and the current value of n. The storage size for n depends on its value, but bits suffice.

This for this song, .

Uh-huh, uh-huh

Is there a song which eliminates even the need to count?

That's the way, uh-huh, uh-huh
I like it, uh-huh, huh

Reference: D. Knuth, `The Complexity of Songs', Comm. ACM, April 1984, pp.18-24

• About this document ...