Steven S. Skiena
Recursion
Recursion is a wonderful, powerful way to solve problems.
Elegant recursive procedures seem to work by magic, but the magic is same reason mathematical induction works!
Example: Prove 
.
For n=1, 
, so its true.
Assume it is true up to n-1.
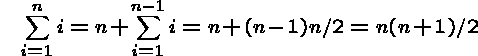
Example: All horses are the same color! (be careful of your basis cases!)
The Tower of Hanoi
MODULE Hanoi EXPORTS Main; (*18.07.94*)
(* Implementation of the game Towers of Hanoi. *)
PROCEDURE Transfer(from, to: Post) =
(*moves a disk from post "from" to post "to"*)
BEGIN
WITH f = posts[from], t = posts[to] DO
INC(t.top);
t.disks[t.top]:= f.disks[f.top];
f.disks[f.top]:= 0;
DEC(f.top);
END; (*WITH f, t*)
END Transfer;
PROCEDURE Tower(height:[0..Height] ; from, to, between: Post) =
(*Does the job through recursive calls on itself*)
BEGIN
IF height > 0 THEN
Tower(height - 1, from, between, to);
Transfer(from, to);
Display();
Tower(height - 1, between, to, from);
END;
END Tower;
BEGIN (*main program Hanoi*)
posts[Post.Start].top:= Height;
FOR h:= 1 TO Height DO
posts[Post.Start].disks[h]:= Height - (h - 1)
END;
Tower(Height, Post.Start, Post.Finish, Post.Temp);
END Hanoi.
To count the number of moves made,
Recursion not only made a complicated problem understandable, it made it easy to understand.
Combinatorial Objects
Many mathematical objects have simple recursive definitions which can be exploited algorithmically.
Example: How can we build all subsets of n items? Build all subsets of n-1 items, copy the subsets, and add item n to each of the subsets in one copy but not the other.
Once you start thinking recursively, many things have simpler formulations, such as traversing a linked list or binary search.
Gray codes
We saw how to generate subsets recursively. Now let us generate them in an interesting order.
All subsets of 
can be represented as binary strings
of length n, where bit i tells whether i is in the subset or not.
Obviously, all subsets must differ in at least one element, or else they would be identical. An order where they differ by exactly one from each other is called a Gray code.
For n=1, {},{1}.
For n=2, {},{1},{1,2},{2}.
For n=3, {},{1},{1,2},{2},{2,3},{1,2,3},{1,3},{3}
Recursive construction algorithm:
Build a Gray Code of 
, make a reverse
copy of it, append n to each subset in the reverse copy, and
stick the two together!
Formulating Recursive Programs
Think about the base cases, the small cases where the problem is simple enough to solve.
Think about the general case, which you can solve if you can solve the smaller cases.
Unfortunately, many of the simple examples of recursion are equally well done by iteration, making students suspicious.
Further, many of these classic problems have hidden costs which make recursion seem expensive, but don't be fooled!
Factorials
PROCEDURE Factorial (n: CARDINAL): CARDINAL =
BEGIN
IF n = 0 THEN
RETURN 1 (* trivial case *)
ELSE
RETURN n * Factorial(n-1) (* recursive branch *)
END (* IF*)
END Factorial;
Be sure you understand how the parameter passing mechanism works.
Would this program work if n was a VAR parameter?
Fibonacci Numbers
The Fibonacci numbers are given by the recurrence relation
.
PROCEDURE Fibonacci(n : CARDINAL) : CARDINAL =
BEGIN (* Fibonacci *)
IF n <= 1 THEN
RETURN 1
ELSE
RETURN Fibonacci(n-1) + Fibonacci(n-2) (*n > 1*)
END (* IF *)
END Fibonacci;
How much time does this elementary Fibonacci function take?
Implementing Recursion
Part of the mystery of recursion is the question of how the machine keeps everything straight.
How come local variables don't get trashed?
The answer is that whenever a procedure or function is called, the local variables are pushed on a stack, so the new recursive call is free to use them.
When a procedure ends, the variables are popped off the stack to restore them to where they were before the call.
Thus the space used is equal to the depth of the recursion, since stack space is reused.
Tail Recursion
Tail recursion costs space, but not time. It can be removed mechanically and is by some compilers.
Moral: Do not be afraid to use recursion if the algorithm is efficient.
The overhead of recursion vs. maintaining your own stack is too small to worry about.
By being clever, you can sometimes save stack space. Consider the following variation of Quicksort:
If (p-1 < h-p) then
Qsort(1,p)
Qsort(p,h)
else
Qsort(p,h)
Qsort(1,p)
By doing the smaller half first, the maximum stack depth
is 
in the worst case.
Applications of Recursion
You may say, ``I just want to get a job and make lots of money. What can recursion do for me?
We will look at three applications
The N-Queens Problem
Backtracking is a way to solve hard search problems.
For example, how can we put n queens on an 
board so
that no two queens attack each other?
Tree Pruning
Backtracking really pays off when we can prove a node early in the search tree.
Thus we need never look at its children, or grandchildren, or great....
We apply backtracking to big problems, so the more clever we are, the more time we save.
There are 
total sets of eight squares
but no two queens can be in the same row.
There are
ways to place eight queens in different rows.
However, since no two queens can be in the same column, there are
only
8! permutations of columns, or only 40,320 possibilities.
We must also be clever to test as quickly as possible the new queen does not violate a diagonal constraint