


Next: About this document
Up: My Home Page
Analytic Tableaux
We next describe an elegant and efficient proof method
for propositional logic that
is based on an analysis of the logical structure
of a given formula.
The analysis is based on the following observations
about the semantics of the logical connectives:
-
- If
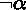 is true, then
is true, then  is false.
is false. - If
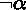 is false, then
is false, then  is true.
is true.
-
- If
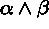 is true, then
is true, then  and
and 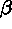 are both true.
are both true. - If
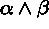 is false, then at least one of
is false, then at least one of  and
and 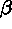 is false.
is false.
-
- If
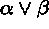 is true, then at least one of
is true, then at least one of  and
and 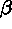 is true.
is true. - If
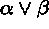 is false, then
is false, then  and
and 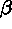 are both false.
are both false.
-
- If
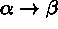 is true, then
is true, then  is false or
is false or 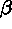 is true.
is true. - If
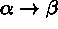 is false, then
is false, then  is true and
is true and 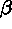 is false.
is false.
Tableaux
A tableau is a binary tree labeled by signed formulas,
that is, expressions of the form 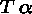 or
or 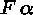 ,
where
,
where  is a propositional formula.
is a propositional formula.
A signed formula 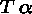 is interpreted as stating that
is interpreted as stating that  is true,
while
is true,
while 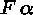 is interpreted as stating that
is interpreted as stating that  is false.
is false.
We know that a formula  is a tautology if, and only if,
its negation
is a tautology if, and only if,
its negation 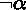 is a contradiction.
is a contradiction.
The method of tableaux consists of constructing a binary tree, starting with
a signed formula 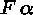 and using tree expansion rules derived
from the above observations,
in an attempt to falsify
and using tree expansion rules derived
from the above observations,
in an attempt to falsify  , i.e., find a truth assignment
that makes
, i.e., find a truth assignment
that makes  false.
false.
If the attempt to falsify  fails,
the formula
fails,
the formula  is a tautology;
otherwise a truth assignment falsifying
is a tautology;
otherwise a truth assignment falsifying  can be extracted from the tableau.
can be extracted from the tableau.
Tableau Construction Rules
Tableaux are constructed by expanding a branch
that contains a signed formula by adding new nodes
as children to the leaf of the branch, according
to the following ``tree expansion'' rules.
-
- If a branch contains a formula
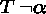 , add a new leaf
, add a new leaf 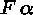 .
. - If a branch contains a formula
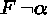 , add a new leaf
, add a new leaf 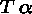 .
.
-
- If a branch contains
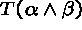 , successively add
new nodes
, successively add
new nodes 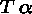 and
and 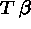 to this branch.
to this branch. - If a branch contains
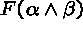 , add
two children,
, add
two children, 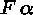 and
and 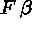 , respectively, to the leaf.
(Thus the branch will be split into two expanded branches.)
, respectively, to the leaf.
(Thus the branch will be split into two expanded branches.)
-
- If a branch contains
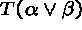 , add
two children,
, add
two children, 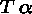 and
and 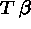 .
. - If a branch contains
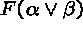 , successively add
new nodes
, successively add
new nodes 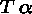 and
and 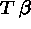 to the same branch.
to the same branch.
-
- If a branch contains
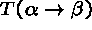 , add
two children,
, add
two children, 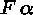 and
and 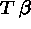 .
. - If a branch contains
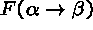 , successively add
new nodes
, successively add
new nodes 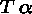 and
and 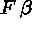 to the same branch.
to the same branch.
A branch of a tableau can be closed
if it contains two nodes labeled by
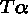 and
and 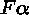 , respectively.
, respectively.
Example
(1) 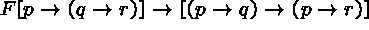
(2) 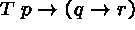 (1)
(1)
(3) 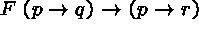 (1)\+
(1)\+
 (4)
(4) 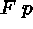 (2)\+
(2)\+
(6) 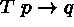 (3)
(3)
mm¯
(7) 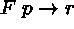 (3)\+
(3)\+
 (10)
(10) 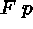 (6)\+
(6)\+
(12) 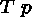 (7)
(7)
[branch closed, 10 & 12]
 (11)
(11) 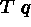 (6)\+
(6)\+
(13) 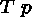 (7)
(7)
[branch closed, 4 & 13]
 (5)
(5) 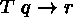 (2)\+
(2)\+
(8) 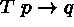 (3)
(3)
(9) 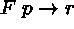 (3)\+
(3)\+
 (14)
(14) 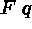 (5)\+
(5)\+
 (16)
(16) 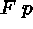 (8)\+
(8)\+
(20) 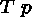 (9)
(9)
[branch closed, 16 & 20]
 (17)
(17) 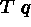 (8)\+
(8)\+
[branch closed, 14 & 8]
 (15)
(15) 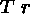 (5)\+
(5)\+
 (18)
(18) 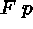 (8)\+
(8)\+
(21) 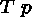 (9)
(9)
[branch closed, 18 & 21]
 (19)
(19) 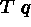 (8)\+
(8)\+
(22) 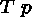 (9)
(9)
(23) 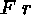 (9)
(9)
[branch closed, 15 & 23]
Indentation indicates tree structure.
Signed formulas are numbered in the order
in which they are generated.
The label to the right of a formula indicates from
which node it was obtained.
(Which rule was applied is uniquely determined
by the formula in question.)
Note that once a rule has been applied to a signed formula it
need not be reapplied along the same branch.
In the example above, tableau construction rules were applied
systematically in a top-down fashion.
That is, a rule was applied to a node only when all
its ancestors (in the tree) had been processed.
A different strategy is to give preference to rules
that do not split a branch.
A corresponding tableau is shown below.
Example: Different Strategy for
Tableau Construction
(1) 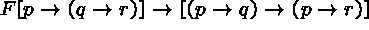
(2) 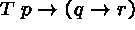 (1)
(1)
(3) 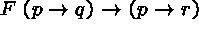 (1)
(1)
(4) 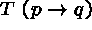 (3)
(3)
(5) 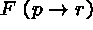 (3)
(3)
(6) 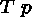 (5)
(5)
(7) 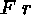 (5)\+
(5)\+
 (8)
(8) 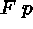 (2)\+
(2)\+
[branch closed, 6 & 8]
 (9)
(9) 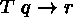 (2)\+
(2)\+
 (10)
(10) 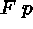 (4)\+
(4)\+
[branch closed, 6 & 10]
 (11)
(11) 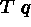 (4)\+
(4)\+
 (12)
(12) 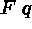 (9)\+
(9)\+
[branch closed, 11 & 12]
 (13)
(13) 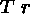 (9)\+
(9)\+
[branch closed, 7 & 13]
Extraction of Truth Assignments from Tableaux
If a branch of a tableau can neither be closed
nor expanded by any new signed formulas,
then a truth assignment can be extracted
under which the initial formula  at the root of the tree is false.
at the root of the tree is false.
Consider the following (partially constructed) tableau:
(1) 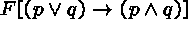
(2) 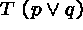 (1)
(1)
(3) 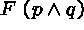 (1)\+
(1)\+
 (4)
(4) 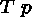 (2)\+
(2)\+
 (6)
(6) 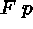 (3)\+
(3)\+
[branch closed, 4 & 6]
 (7)
(7) 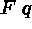 (3)\+
(3)\+
[branch done]
 (5)
(5) 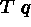 (2)\+
(2)\+
[ ...]
The branch from the root (1) to leaf (7) has been fully
expanded, in that no expansion along this branch will
introduce new formulas.
From this branch we can extract a truth assignment -
assigning T to p according to (4)
and F to q according to (7) -
under which the initial formula
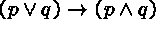 is false.
The formula is therefore not a tautology.
is false.
The formula is therefore not a tautology.
Example
The following (15-node) tableau shows that
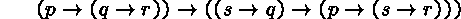
is a tautology:
(1) 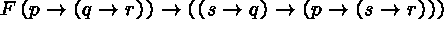
(2) 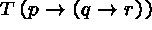 (1)
(1)
(3) 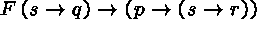 (1)
(1)
(4) 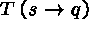 (3)
(3)
(5) 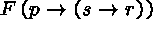 (3)
(3)
(6) 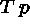 (5)
(5)
(7) 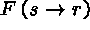 (5)
(5)
(8) 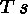 (7)
(7)
(9) 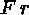 (7)\+
(7)\+
 (10)
(10) 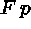 (2)\+
(2)\+
[branch closed, 6 & 10]
 (11)
(11) 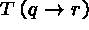 (2)\+
(2)\+
 (12)
(12) 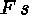 (4)\+
(4)\+
[branch closed, 8 & 12]
 (13)
(13) 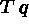 (4)\+
(4)\+
 (14)
(14) 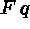 (11)\+
(11)\+
[branch closed, 13 & 14]
 (15)
(15) 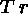 (11)\+
(11)\+
[branch closed, 9 & 15]
A truth table for the given formula would consist of
16 lines (as the formula contains 4 variables),
but each line depends on 7 non-trivial subformulas,
so that a total of 7*16=112 evaluations may be required for
the complete truth table.



Next: About this document
Up: My Home Page
Steve Skiena
Tue Aug 24 15:32:11 EDT 1999
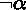 is true, then
is true, then  is false.
is false.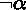 is false, then
is false, then  is true.
is true.
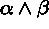 is true, then
is true, then  and
and 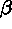 are both true.
are both true.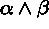 is false, then at least one of
is false, then at least one of  and
and 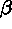 is false.
is false.
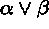 is true, then at least one of
is true, then at least one of  and
and 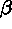 is true.
is true.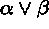 is false, then
is false, then  and
and 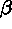 are both false.
are both false.
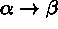 is true, then
is true, then  is false or
is false or 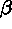 is true.
is true.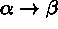 is false, then
is false, then  is true and
is true and 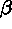 is false.
is false.