Logical Consequence

We say that logically implies , or that is a logical consequence of , if is true whenever is true.

Example: p logically implies .

Proof:

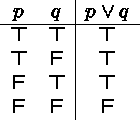
Note that logical consequence is a weaker condition than logical equivalence.

Theorem: A formula logically implies if and only if is a tautology.

This gives us a tool to infer truths!

A rule of inference is a rule of the form: ``From premises , infer conclusion ''

A rule of inference is sound or valid if the conclusion is a logical consequence of the conjunction of all premises.

A rule of inference is unsound or bogus if it isn't!

Modus Ponens

If we assume that (1) if it is raining then today must be Monday, and (2) it is raining, then we can conclude that (3) today must be Monday.

But why?

Let r denote the proposition "it is raining" and m denote "today must be Monday".

Then is a tautology, so m is a logical consequence of and r.

Modus Ponens (Latin for ``method of affirming'') is the following inference rule:

From and , infer .

Modus Tollens

If we assume that (1) if it is raining then today must be Monday, and (2) if it is not Monday, then we can conclude that (3) it is not raining.

Why? Because is a tautology.

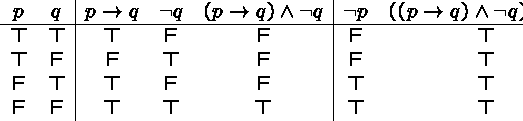
Modus Tollens (Latin for ``method of denying''):

From and , infer .

Cognative Psychologists have shown that under 60% of college students have a solid intuitive understanding of Modus Tollens (versus almost 100% for Modus Ponens).

Invalid Reasoning Example

If we assume that (1) if it is raining, then today must be Monday, and (2) it is not raining, can we conclude that (3) today is not Monday?

In other words, is the following inference rule sound? ``From and , infer .''

No! - because is not a tautology.

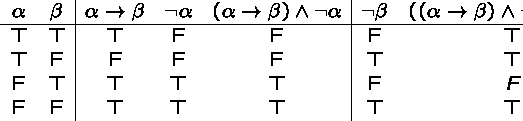
This fails when both and are true.

Transitivity of Implication

From and , infer :

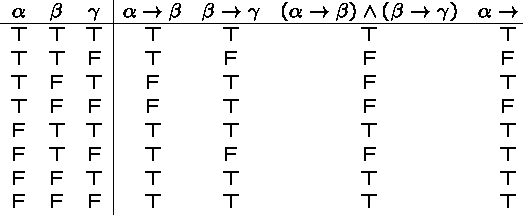
This inference rule is also called ``hypothetical syllogism''.

Sherlock Holmes in Action

``And now we come to the great question as to the reason why. Robbery has not been the object of this murder, for nothing was taken. Was it politics, or was it a woman? That is the question confronting me. I was inclined from the first to the latter supposition. Political assassins are only too glad to do their work and fly. This murder had, on the contrary, been done most deliberately and the perpetrator had left his tracks all over the room, showing he had been there all the time.'' - A. Conan Doyle, A Study in Scarlet

What did Sherlock Holmes conclude?

Propositions and Premises

We can break the story into the following propositions:

• P1: It was robbery.
• P2: Nothing was taken.
• P3: It was politics.
• P4: It was a woman.
• P5: The assassin left immediately.
• P6: The assassin left tracks all over the room.

Holmes identifies the following premises defined on these propositions:

• 
• P2
• 
• 
• 
• P6

Conclusion: P4!

Valid or Invalid Arguments?

• If Elvis is the king of rock and roll, then Elvis lives. Elvis is the king. Therefore Elvis is alive. Valid or invalid?

  This argument is valid, in that the conclusion is established (by Modus ponens) if the premises are true. However, the first premise is not true. Therefore the conclusion is false - but that is none of our business.

• If the stock market keeps going up, then I'm going to get rich. The stock market isn't going to keep going up. Therefore I'm not going to get rich. Valid or invalid?

  This argument is invalid, specifically an inverse error. Its form is from and infer . This yields an inverse error.

• If New York is a big city, then New York has tall buildings. New York has tall buildings. Therefore New York is a big city. Valid or invalid?

  This argument is invalid, even though the conclusion is true. Its form is from and q, infer p.

Proof by Contradiction

Suppose that we want to prove , and we know is true. Instead of proving directly, we may instead show that assuming leads to a contradiction.

Formally, from and , infer .

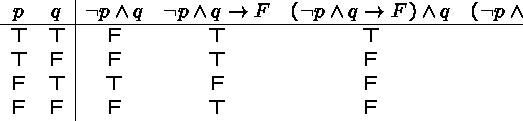
Example: ``Suppose I did shoot him. Well then I had to be in the room at the time of the crime to shoot him. However, at that exact time, I was teaching CSE113 before over a hundred witnesses. Therefore I couldn't have been the one to shoot him.''

There are beautiful examples of proof by contradiction in number theory.

Proofs by contradiction are very susceptible to reasoning errors unless you do them formally.

Make sure that your contradiction depends upon your assumption - otherwise it means that either your assumption was unnecessarily strong or (more likely) that you botched your reasoning.

Proof by contradiction is sometime also called ``reductio ad absurdum'' or ``indirect proof''.

From Inspector Craig's Files

A large sum of money has been stolen from the store. The criminal(s) were seen driving off from the scene. From questioning criminals A, B, and C we know:

1. No one other than A, B, or C were involved in the robbery.
2. C never pulls a job without using A.
3. B does not know how to drive.

Is A innocent or guilty? Let a, b, and c represent the respective propositions that A or B or C is guilty.

From the story, we have the following assumptions:

1. 
2. 
3. 

Proof: (by contradiction)

Assume a is innocent, i.e .

By the contrapositive of (2) and modus ponens, we may infer .

We thus have , which by De Morgan's Law is logically equivalent to .

By the contrapositive of (3) and modus ponens, we may infer .

We now have and and , which contradict assumption (1).

Thus we may conclude that a is true, which means that A is guilty!

Generalizing and Particularizing

Any man or woman is a person. Suppose I am a man. Therefore I am a person.

The inference rule disjunctive addition is a tool for generalizing: From p, infer .

Suppose that it is raining and snowing. Therefore it is raining.

The inference rule conjunctive simplification is a tool for particularizing: From , infer p.

Case Analysis

Suppose that I either a man or a woman. I am not a woman. Therefore I am a man.

The inference rule disjunctive syllogism is a tool for case analysis: from and , infer q.

Now suppose that I am either a man or a woman. Being a man means I am a person. Being a Woman means that I am person. Therefore I am a person.

The inference rule of division into cases represents a more sophisticated case analysis: From , , and , infer r.

• About this document ...