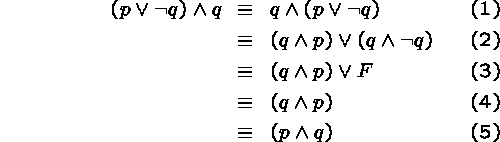Logical Equivalence
If two formulas evaluate to the same truth value in all situations, so that their truth tables are the same, they are said to be logically equivalent.
We write 
to indicate that
two formulas 
and 
are logically equivalent.
If two formulas are logically equivalent, their syntax may be different, but their semantics is the same. The logical equivalence of two formulas can be established by inspecting the associated truth tables.
Is 
logically equivalent to 
?
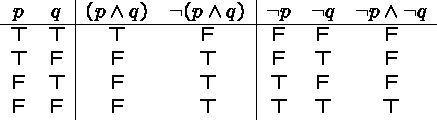
Lines 2 and 3 prove that this is not the case.
Substituting logically inequivalent formulas is the source of most real-world reasoning errors.
Is logically equivalent to 
?
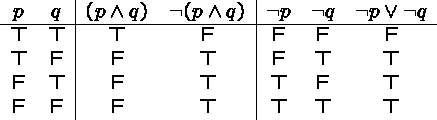
Yes, 
.
De Morgan's Laws
There are a number of important equivalences, including the following De Morgan's Laws:
These equivalences can be used to transform a formula into a logically equivalent one of a certain syntactic form (called a ``normal form'').
Another useful logical equivalence is double negation:
Example:
The first equivalence is by double negation (as equivalence can be used in both directions), the second by De Morgan's Law.
Note that we have just derived a new equivalence,
which shows that disjunction can be expressed in terms of conjunction and negation!
Some Logical Equivalences
You should be able to convince yourself of (i.e., prove) each of these:
Commutativity of 
: 
Commutativity of 
: 
Associativity of : 
Associativity of : 
Idempotence: 
Absorption: 
Distributivity of : 
Distributivity of : 
De Morgan's Law for : 
De Morgan's Law for : 
Double Negation: 
Contradictions: 
Identities: 
Tautologies: 
Tautologies and Contradictions
A tautology is a formula that is always true, no matter which truth values we assign to its variables.
Consider the proposition ``I passed the exam or I did not pass the exam,''
the logical form of which is represented by the formula 
.
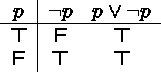
This is a tautology, as we get T in every row of its truth table.
A contradiction is a formula that is always false.
The logical form of the proposition ``I passed the exam and I did not pass the exam''
is represented by 
.
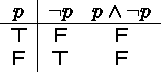
Tautologies and contradictions are related.
Theorem: If is a tautology (contradiction)
then 
is a contradiction (tautology).
Implication
Syntax: If and are formulas, then
(read `` implies '')
is also a formula.
We call the premise
and the conclusion
of the implication.
Semantics: If is true and is false, then
is false. In all other cases, is true.
Truth table:
Example:
: If you get A's on all exams, then you will get an
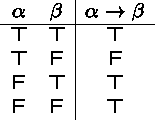
A in the course.
The semantics of implication is trickier than for the other connectives.
and are both true, clearly the implication is true. is true but is false, the implication is clearly false! is false
no conclusion can be drawn,
but both being true and being false
are consistent,
so that the implication is true in both cases.
Implication can also be expressed by other connectives,
for example,
is logically equivalent to
.
Prosecutor: ``If the defendant is guilty, then he had an accomplice.''
Defense Attorney: ``That's not true!!''
What did the defense attorney just claim??
Biconditional
Syntax: If and are formulas, then
(read `` if and only if (iff) '')
is also a formula.
Semantics: If and are either both true or both false, then
is true. Otherwise, is false.
Truth table:
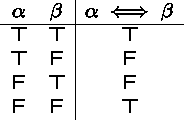
Example:
: Bill will get an A if and only if Bill studies hard.
The biconditional may be viewed as a shorthand for a conjunction of two implications, as
is logically equivalent to
.
Necessary and Sufficient Conditions
The phrase ``necessary and sufficient conditions'' appears often in mathematics.
A proposition is necessary for if cannot be true
without it: 
is a tautology.
Example: It is necessary for a student to have a 2.8 GPA in the core courses to be admitted to become a CSE major.
A proposition is sufficient for if
is a tautology.
Example: It is sufficient for a student to get A's in CSE 113, CSE 114, CSE 213, CSE 214, and CSE 220 in order to be admitted to become a CSE major.
Theorem
If a proposition
Tautologies and Logical Equivalence
Theorem: A propositional formula is logically equivalent to if and only if
is a tautology.
Proof:
(a)
If is a tautology, then is logically
equivalent to .
Why?
If is a tautology,
then it is true for all truth assignments.
By the semantics of the biconditional,
this means that and agree on every row
of the truth table. Hence the two formulas are logically equivalent.
(b)
If is logically equivalent to , then
is a tautology.
Why?
If and are logically equivalent,
then they evaluate to the same truth value
for each truth assignment.
By the semantics of the biconditional,
the formula is true in all situations.
height6pt width4pt
Related Implications
Implication: : If you get A's on all exams, you get an A in the course.
Converse: 
.
If you get an A in the course, then you got A's on all exams.
Inverse: 
.
If you didn't get A's on all exams, then you didn't get an A in the course.
Contrapositive: 
.
If you didn't get an A in the course, then you didn't get A's on all exams.
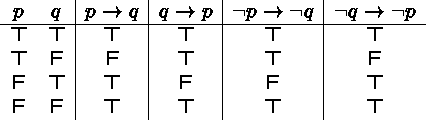
Note that implication is logically equivalent to the contrapositive, and that the inverse is logically equivalent to the converse!
Deriving Logical Equivalences
We can establish logical equivalence either symbolically or via truth tables.
Example: is logically
equivalent to 
.
Symbolic proofs are much like the simplifications you did in high school algebra - trial-and-error leads to experience and finally cunning.
Example: 
Proof: (which laws are used at each step?)
