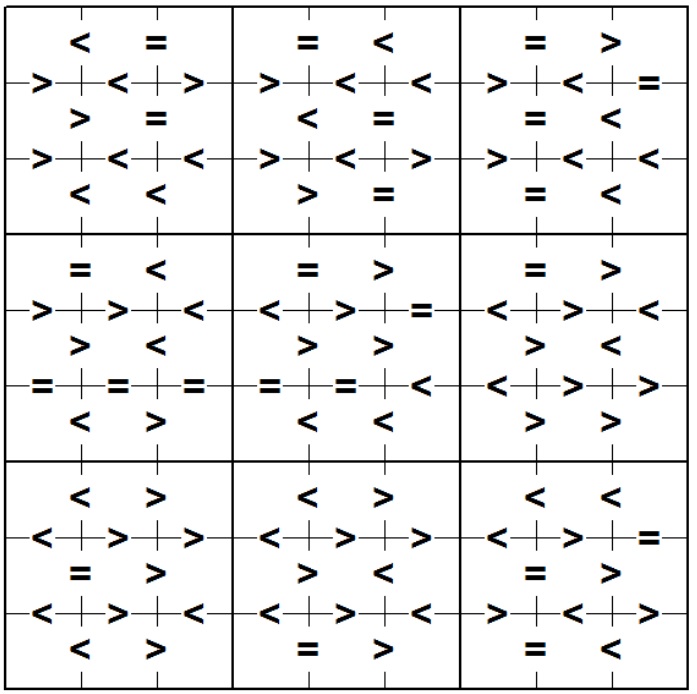
Tony schedules the conference talks for the conference. The aim is to fill in a 9 days of 9 slots grid with the talks of lengths from 1 through 9 minutes so that each digit 1 through 9 occurs exactly once in each row, exactly once in each column and exactly once in each of the 9 3-by-3 sub-squares subject to the following constraints. The constraints are on the sum of adjacent squares within each 3-by-3 sub-square. In the illustration below, the symbols <, = and > indicate that the sum of the values on either side (or above and below), the symbol must have sum less than 10, equal to 10 or greater than 10, respectively.

However, Tony finds out that the solutions for his scheduling is not unique. Your problem is to find how many different solutions satisfy all the constraints of the problem: row, column, 3-by-3 box and inequality constraints.
An input file for LP systems contains the following facts:
row(Number,S1,S2,S3,S4,S5,S6) containing the row number (1, 3, 5, 6, 8, 10, 11, 13 and 15) and 6 digits corresponding to constraints on the sum of values to the left and right of the symbol. In order to standardize the way we represent the three relations (<, = and >), we will use the integers -1, 0, 1 to represent <, = and >.vertical(Number,S1,S2,S3,S4,S5,S6,S7,S8,S9) containing the row number (2, 4, 7, 9, 12 and 14) and 9 digits corresponding to constraints on the sum of values above and below the symbol.Example input for the figure above:
row(1,-1,0,0,-1,0,1).
vertical(2,1,-1,1,1,-1,-1,1,-1,0).
row(3,1,0,-1,0,0,-1).
vertical(4,1,-1,-1,1,-1,1,1,-1,-1).
row(5,-1,-1,1,0,0,-1).
row(6,0,-1,0,1,0,1).
vertical(7,1,1,-1,-1,1,0,-1,1,-1).
row(8,1,-1,1,1,1,-1).
vertical(9,0,0,0,0,0,-1,-1,1,1).
row(10,-1,1,-1,-1,1,1).
row(11,-1,1,-1,1,-1,-1).
vertical(12,-1,1,1,-1,1,1,-1,1,0).
row(13,0,1,1,-1,0,1).
vertical(14,-1,1,-1,-1,1,-1,1,-1,1).
row(15,-1,1,0,1,0,-1).
The output should contain exactly one fact of the form solutions(S), where S is the number of different solutions for the input problem.
Acknowledgment: thanks to Annie Liu for suggesting related problems.