Elevators

(Main file name: elevator.pl)

The Empire State Building has N elevators. Each elevator is connecting exactly two floors and it does not stop on the floors between that two floors. The speed of all the elevators is the same: 1 second to pass one floor. In the beginning, each elevator is in its lower position and they are starting cruising to the upper floor. After some elevator come to its upper position, it immediately starts to go back to its lower position, and so on. Peter is on the lowest floor 0 (zero) and he wants to go to the top floor as soon as possible. He can change elevators only on the floors that are common to both elevators. The elevators are constantly moving, so Peter has to wait sometimes for the next elevator. If the other elevator is in that moment on that floor, that change does not take any time. The goal is to find out the quickest possible time that Peter can reach the top floor.

Input Format

An input file for contains the following facts:

One fact of the form top(K), which specifies the highest floor, and goal,
One fact of the form elevators(N), which specifies the number of elevators,
For each I in 1..N, there is a fact of the form elevator(I,B,T), where I is the elevator number, B is the starting floor of the elevator, and T is the top floor of the elevator,

The input data guarantees that a solution exists.

Output format

The output should contain exactly one fact of the form min_time(S), where S is the minimum amount of time Peter can make it to the top floor.

Examples

Input	Output
top(10). elevators(4). elevator(1,0,5). elevator(2,5,10). elevator(3,5,7). elevator(4,7,10).	min_time(15).
top(10). elevators(4). elevator(1,0,5). elevator(2,5,10). elevator(3,5,8). elevator(4,8,10).	min_time(14).
top(19). elevators(10). elevator(1,0,6). elevator(2,6,19). elevator(3,3,6). elevator(4,3,9). elevator(5,9,19). elevator(6,3,13). elevator(7,13,17). elevator(8,17,19). elevator(9,9,17). elevator(10,6,17).	min_time(30).
top(10). elevators(5). elevator(1,0,6). elevator(2,2,6). elevator(3,6,8). elevator(4,8,10). elevator(5,6,10).	min_time(12).
top(10). elevators(5). elevator(1,0,3). elevator(2,2,6). elevator(3,0,2). elevator(4,3,10). elevator(5,6,10).	min_time(20).
top(12). elevators(5). elevator(1,0,3). elevator(2,5,10). elevator(3,3,8). elevator(4,8,12). elevator(5,8,12).	min_time(20).
top(15). elevators(6). elevator(1,0,6). elevator(2,0,8). elevator(3,3,8). elevator(4,1,3). elevator(5,6,15). elevator(6,8,15).	min_time(21).
top(15). elevators(5). elevator(1,0,3). elevator(2,7,10). elevator(3,3,7). elevator(4,3,10). elevator(5,10,15).	min_time(25).

How?
Use Case 1: Peter takes the elevator 1 from floor 0 to floor 5. Here, he has 2 options:
Case 1.1: Peter waits 5 seconds for elevator 2 to come down back to 5 (because by the time Peter gets to floor 5, the elevator 2 is up to floor 10). He takes the elevator 2 and gets to floor 10 at second 15.
Case 1.2: Peter waits 3 seconds for elevator 3 to come down back to 5 (because by the time Peter gets to floor 5, the elevator 3 is at floor 6 going up). He takes the elevator 3 and gets to floor 7 at second 10. The elevator 4 is at floor 9 going down, so Peter has to wait 2 seconds to take it. Peter gets to floor 10 at second 15.

Use Case 2: Peter takes the elevator 1 from floor 0 to floor 5. Here, he has 2 options:
Case 2.1: Peter waits 5 seconds for elevator 2 to come down back to 5 (because by the time Peter gets to floor 5, the elevator 2 is up to floor 10). He takes the elevator 2 and gets to floor 10 at second 15.
Case 2.2: Peter waits 1 second for elevator 3 to come down back to 5 (because by the time Peter gets to floor 5, the elevator 3 is at floor 6 going down). He takes the elevator 3 and gets to floor 8 at second 8. Elevator 4 is at floor 9 going up, so Peter has to wait 3 seconds. Peter gets to floor 10 at second 14.
Note: Sometimes Peter can also choose to go down with some elevators, like in this case:
elevator(1,0,3).
elevator(2,2,3).
elevator(3,2,10).
In this case, Peter will go from floor 0 to floor 3, then from floor 3 to floor 2, and then from floor 2 to floor 10

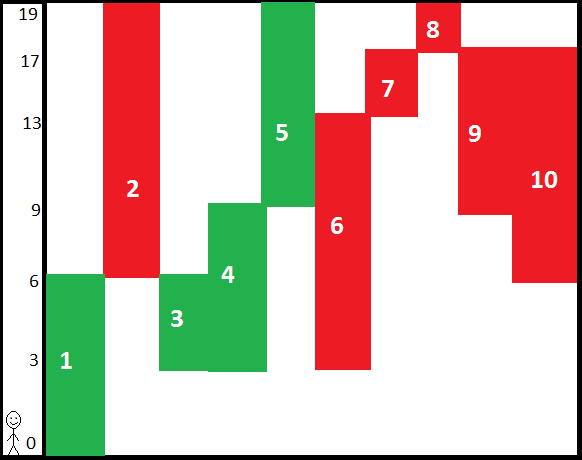
Use Case 3: Peter takes elevator 1 from floor 0 to 6. His optimal solution is to wait for elevator 3, and take it down to floor 3. Then he must immediately take elevator 4 up to floor 9. He waits for 2 seconds, then takes elevator 5 up to floor 19 to finish in 30 seconds.
Diagram for case 3: