Ranger - Nearest Neighbor Search in Higher Dimensions
Ranger is a tool for visualizing and experimenting with
nearest neighbor and orthogonal range queries in high-dimensional data sets,
using multidimensional search trees.
It was developed by Michael Murphy as his masters project under Steven
Skiena at Stony Brook.Four different search data structures are supported by Ranger:
-
Naive k-d -- the original kd-tree defined by Bentley,
"Multidimensional Binary Search Trees Used for Associative Searching"
ACM Sept. 1975 Vol. 18. No. 9
-
Median k-d -- A refined kd-tree, using median cuts and bucketing,
discussed in J.H. Friedman, J.L. Bentley, R.A. Finkel
"An Algorithm for Finding Best Matches in Logarithmic Expected Time"
ACM Transactions of Mathematical Software Vol 3 No. 3 Sept. 1977
pp. 209-226
-
Sproull k-d -- Sproull's variant of the $kd$-tree.
The choice of partition plane is not orthogonal, rather,
it is selected by the principal eigenvector of
the covariance matrix of the points.
R.F. Sproull
"Refinements to Nearest-Neighbor Searching in k-Dimensional Trees"
J. Algorithmica 1990. pp. 579-589
-
VP-tree - The vantage point tree is a data structure that chooses
vantage points to perform a spherical decomposition of the search space.
Yianilos claims this method is suited for
non-Minkowski metrics (unlike kd-trees)
and for lower dimensional objects embedded
in a higher dimensional space.
P.N. Yianilos
"Data Structures and Algorithms for Nearest Neighbor Search in General Metric
Spaces"
SODA '93
Ranger supports queries in up to 25 dimensions for all data structures,
under any Minkowski metric.
Each of these data structures can be applied each of several different
applications, including $k$-nearest neighbor graphs and
orthogonal range queries.
Timing data and algorithm animations can be used to
study the performance of these data structures.
Because kd-trees are heuristic data structures, their performance
can be dramatically effected by the distribution of the data.
{\em Ranger} includes generators for a variety of distributions
in arbitrary dimensions, including several degenerate distributions
Bentley has
noted tend to frustrate heuristic data structures.
Ranger provides a number of features to aid in
visualizing multi-dimensional data.
Arbitrary two- or three-dimensional projections of a higher dimensional
data set can be viewed.
To identify the most appropriate projection at a glance,
Ranger provides a d*d matrix of all two-dimensional
projections of the data set.
In any three-dimensional projections, rotation along arbitrary axes
can be used to facilitate understanding.
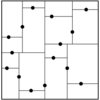
For each of the four search data structures,
a graphic representation of the space division is provided.
This provides considerable insight into the appropriateness of
a data structure for a particular distribution.
Ideally, the search space is decomposed into fat, regularly-sized regions,
but this is often not possible with degenerate distributions.
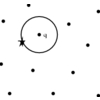
Further, Ranger can animate a nearest-neighbor search, by highlighting
each region as it is visited, for any two- or three-dimensional projection.
Ranger is written in C, using Motif.
It runs on Silicon Graphics and HP workstations.
Download Files (local site)
Problem Links
This page last modified on 2008-07-10
.
www.algorist.com