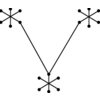
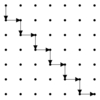
1.5.10 Steiner Tree
INPUT OUTPUT
Input Description:
A graph G=(V,E).
A subset of vertices T \in V.
Problem:
Find the smallest tree connecting all the vertices of T.
Excerpt from
The Algorithm Design Manual:
Steiner tree often arises in network design and
wiring layout problems.
Suppose we are given a set of sites that must be connected
by wires as cheaply as possible.
The minimum Steiner tree describes the
way to connect them using the smallest amount of wire.
Analogous problems arise in designing networks of water pipes or
heating ducts in buildings.
Similar considerations also arise in VLSI circuit layout,
where we seek to connect a set of sites to (say)
ground under constraints such as material cost, signal propagation time,
or reducing capacitance.
The Steiner tree problem is distinguished from the minimum spanning tree problem in that we are permitted to
construct or select intermediate connection points to reduce the cost of the tree.
Recommended Books
Related Links
COIN|OR: COmputational INfrastructure for Operations Research
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
The Steiner Tree Problem: a tour through graphs,
algorithms, and complexity
Advances in Steiner Trees
The Steiner Tree Problem
Computational Geometry
Combinatorial Optimization: Networks and Matroids
