1.3.2 Searching
INPUT OUTPUT
Input Description:
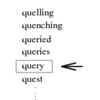
A set S of n keys, a query key q.
Problem:
Where is q in S?
Excerpt from
The Algorithm Design Manual:
We treat searching here as a problem distinct from dictionaries because simpler and more efficient solutions emerge
when our primary interest is static searching. These little data structures can yield large performance
improvements when properly employed in an innermost loop. Also, several of the ideas from list and array searching,
such as binary search and self-organization, apply to other problems and justify our attention.
There are two basic approaches to array searching: sequential search and binary search. Both are simple, yet
have interesting and subtle variations. In sequential search, we simply start from the front of our list
or array of keys and compare each successive item against the key until we find a match or reach the end. In
binary search, we start with a sorted array of keys. To search for key $q$, we compare $q$ to the
middle key $S_{n/2}$. If $q$ is before $S_{n/2}$, it must reside in the top half of our set; if not, it must
reside in the bottom half of our set. By repeating this process on the correct half, we find the key in a
total of $\lceil \lg n \rceil$ comparisons. This is a big win over the $n/2$ comparisons we expect with
sequential search.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Data Structures and Algorithm Analysis in C++ (3rd Edition)
Handbook of Data Structures and Applications
The Art of Computer Programming : Sorting and Searching
The Art of Computer Programming: Fundamental Algorithms
Handbook of Algorithms and Data Structures
Constructive Combinatorics
The Design and Analysis of Computer Algorithms
