1.6.5 Nearest Neighbor Search
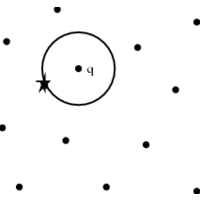
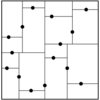
INPUT OUTPUT
Input Description:
A set S of n points in d dimensions;
a query point q.
Problem:
Which point in S is closest to q?
Excerpt from
The Algorithm Design Manual:
The need to quickly find the nearest neighbor to a query point
arises in a variety of geometric applications.
The classic example in two dimensions is designing a system to dispatch
emergency vehicles to the scene of a fire.
Once the dispatcher learns the location of the fire,
she uses a map to find the firehouse closest to this point
so as to minimize transportation delays.
This situation occurs in any application mapping customers to service
providers.
Nearest-neighbor search is also important in classification.
Suppose we are given a collection of data about people (say age, height, weight,years of education, sex, and
income level)
each of whom has been labeled as Democrat or Republican.
We seek a classifier to decide which way a different person is
likely to vote.
Each of the people in our data set is represented by a
party-labeled point in $d$-dimensional space.
A simple classifier can be built by assigning to the new point
the party affiliation of its
nearest neighbor.
Such nearest-neighbor classifiers are widely used, often in high-dimensional
spaces.
The vector-quantization method of image compression partitions an image
into 8 X 8 pixel regions.
This method uses a predetermined library of several
thousand 8 X 8 pixel tiles and replaces each image region
by the most similar library tile.
The most similar tile is the point in 64-dimensional space that is
closest to the image region in question.
Compression is achieved by reporting the identifier of the closest
library tile instead of the 64 pixels,
at some loss of image fidelity.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Algorithms from P to NP, Vol. I: Design and Efficiency
Introduction to Algorithms
Applications of spatial data structures
Introduction to Algorithms
