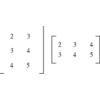1.2.1 Solving Linear Equations
INPUT OUTPUT
Input Description:
An m x n matrix A, and an m x 1 vector b,
representing m linear equations with n variables.
Problem:
What is the vector x such that A \cdot x = b?
Excerpt from
The Algorithm Design Manual:
Solving linear systems is a problem of such scientific and commercial importance that excellent codes are readily
available. There is likely no good reason to implement your own solver, even though the basic algorithm (Gaussian
elimination) is one we learned in high school. This is especially true if you are working with large systems.
Gaussian elimination is based on the fact that the solution to a system
of linear equations is invariant under scaling (multiplying both sides by a constant;
i.e. if x=y, then 2x=2y) and adding equations (i.e. the solution to
the equations x=y and w=z is the same as the solution to x=y and x+w=y+z).
Gaussian elimination scales and adds equations so as to eliminate each variable from all but one equation,
leaving the system in such a state that the solution can just be read off from the equations.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Parallel Numerical Algorithms
Matrix Computations
Elementary Numerical computing with Mathematica
Numerical methods and analysis
Introduction to Algorithms
Introduction to Parallel and Vector Solution of Linear Systems
The Design and Analysis of Computer Algorithms
