1.2.9 Arbitrary Precision Arithmetic
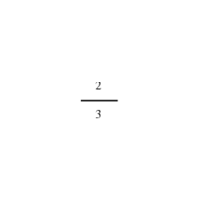
INPUT OUTPUT
Input Description:
Two very large integers, x and y.
Problem:
What is x+y, x-y, x x y and x / y?
Excerpt from
The Algorithm Design Manual:
Any programming language whose level rises above basic assembler supports single- and perhaps
double-precision integer/real addition, subtraction, multiplication, and division. But what if we wanted to
represent the national debt of the United States in pennies? One trillion dollars worth of pennies requires
15 decimal digits, which is far more than can fit into a 32-bit integer.
In other applications much larger integers are needed. The RSA algorithm for public-key cryptography
requires integer keys of at least 100 digits to achieve any level of security, and 1000 digits are
recommended. Experimenting with number-theoretic conjectures for fun or research always requires playing with
large numbers.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
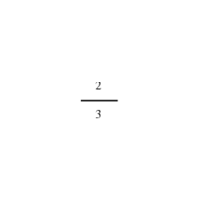
A Computational Introduction to Number Theory and Algebra
Algorithms in Java, Third Edition (Parts 1-4)
The Art of Computer Programming : Seminumerical Algorithms
Algorithmic Number Theory : Efficient Algorithms
Introduction to Algorithms
Introduction to Algorithms
The Design and Analysis of Computer Algorithms
