About the Book

The Stony Brook Algorithm Repository

Steven Skiena
Stony Brook University
Dept. of Computer Science

1.3.6 Generating Partitions

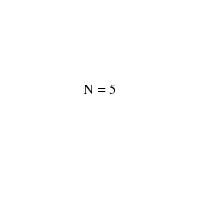
INPUT                    OUTPUT

Input Description: An integer n.

Problem: Generate (1) all, or (2) a random, or (3) the next integer or set partitions of length n.

Excerpt from The Algorithm Design Manual: There are two different types of combinatorial objects denoted by the term ``partition'', namely integer partitions and set partitions. Although they are quite different beasts, it is a good idea to make both a part of your vocabulary:

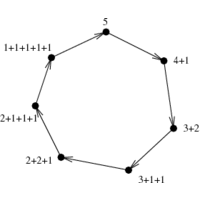
Integer partitions of n are sets of nonzero integers that add up to exactly n. For example, the seven distinct integer partitions of 5 are {5}, {4,1}, {3,2}, {3,1,1}, {2,2,1}, {2,1,1,1}, and {1,1,1,1,1}. An interesting application I encountered that required the generation of integer partitions was in a simulation of nuclear fission. When an atom is smashed, the nucleus of protons and neutrons is broken into a set of smaller clusters. The sum of the particles in the set of clusters must equal the original size of the nucleus. As such, the integer partitions of this original size represent all the possible ways to smash the atom.
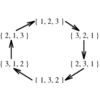
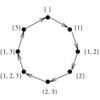
Set partitions divide the elements 1,\ldots,n into nonempty subsets. For example, there are fifteen distinct set partitions of n=4: {1234}, {123,4}, {124,3},{12,34},{12,3,4},{134,2},{13,24},{13,2,4},{14,23},{1,234},{1,23,4},{14,2,3},{1,24,3}, {1,2,34}, and {1,2,3,4}. Several of the problems in this catalog return set partitions as results, such as vertex coloring and connected components.