1.5.11 Feedback Edge/Vertex Set
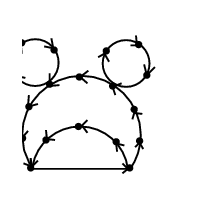
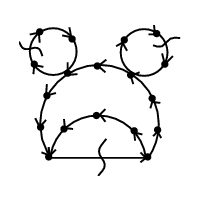
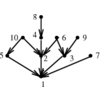
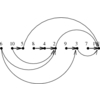
INPUT OUTPUT
Input Description:
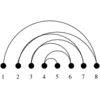
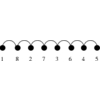
A (directed) graph G=(V,E).
Problem:
What is the smallest set of edges E' or vertices V' whose
deletion leaves an acyclic graph?
Excerpt from
The Algorithm Design Manual:
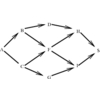
Feedback set problems arise because many algorithmic problems
are much easier or much better defined on directed acyclic graphs than
on arbitrary digraphs. Topological sorting can be used to test whether a graph is a DAG, and if so, to order the
vertices so as to respect the edges as precedence scheduling constraints. But how can you design a schedule if
there are cyclic constraints, such as A must be done before B, which must be done before C,
which must be done before A?
By identifying a feedback set, we identify the smallest number of constraints that must be dropped so as to permit
a valid schedule. In the feedback edge (or arc) set problem, we drop precedence constraints (job A
must come before job B). In the feedback vertex set problem, we drop entire jobs and any
associated constraints. It is also referred to in the literature as the maximum acyclic subgraph problem.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
The Stanford Graphbase : A Platform for Combinatorial Computing
Graph Algorithms
Computers and Intractability: A Guide to the Theory of NP-Completeness
The Design and Analysis of Computer Algorithms
