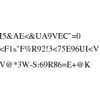1.2.8 Factoring and Primality Testing
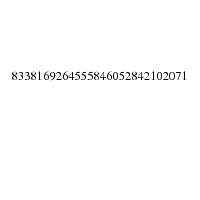
INPUT OUTPUT
Input Description:
An integer n.
Problem:
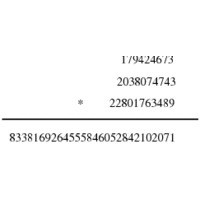
Is n a prime number, and if not what are the factors of n?
Excerpt from
The Algorithm Design Manual:
Although factoring and primality testing are related problems, algorithmically they are quite different.
There exist algorithms that can demonstrate that an integer is composite (i.e. not prime) without
actually giving the factors. To convince yourself of the plausibility of this, note that you can demonstrate
the compositeness of any nontrivial integer whose last digit is 0, 2, 4, 5, 6, or 8 without doing the actual
division.
The simplest algorithm for both of these problems is brute-force trial division.
To factor n, compute the remainder of n/i for all 1 < i \leq \sqrt{n}. The prime
factorization
of
n will contain at least one instance of every i such that n/i = \lfloor n/i \rfloor,
unless n is prime. Make sure you handle the multiplicities correctly and account for any primes larger
than \sqrt{n}.
Considerably faster factoring algorithms exist, whose correctness depends upon more substantial number
theory. The fastest known algorithm, the number field sieve, uses randomness to construct a system
of congruences, the solution of which usually gives a factor of the integer. Integers with as many at 128
digits have been factored using this method, although such feats require enormous amounts of computation.
Recommended Books
Related Links
The Prime Pages
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
A Computational Introduction to Number Theory and Algebra
Prime Numbers: A Computational Perspective
Primality Testing in Polynomial Time: From Randomized Algorithms to "PRIMES Is in P"
Primality Testing and Integer Factorization in Public-Key Cryptography
Computers and Intractability: A Guide to the Theory of NP-Completeness
