1.4.11 Drawing Trees
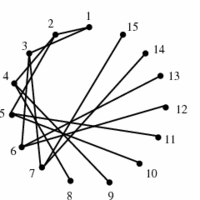
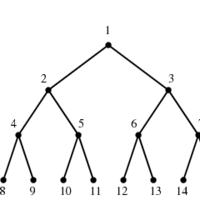
INPUT OUTPUT
Input Description:
A tree (ie. graph without any cycles) T.
Problem:
A nice drawing of the tree T.
Excerpt from
The Algorithm Design Manual:
There are as many reasons to want to draw trees as there are types of structures that trees represent.
Consider software and debugging tools that illustrate the hierarchical structure of file system directories, or
that trace the execution
The primary issue in drawing trees is establishing whether you are
drawing free or rooted trees:
- Rooted Trees define a hierarchical order, emanating from
a single source node identified as the root. Any drawing must reflect this hierarchical structure, as well as any
additional application-dependent constraints on the order in which children must appear. For example, family trees
are rooted, with sibling nodes typically drawn from left to right in the order of birth.
- Free trees do not encode any structure beyond their connection topology.
For example, there is no root associated with the minimum spanning tree of any graph, so a hierarchical drawing can
be misleading. Such free trees might well inherit their drawing from that of the full underlying graph, such as the
map of the cities whose distances define the minimum spanning tree.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Handbook of Graph Drawing and Visualization
Graph Drawing Software
Drawing Graphs: Methods and Models
Graph Drawing: Algorithms for the Visualization of Graphs
Computational Discrete Mathematics: Combinatorics and Graph Theory with Mathematica
