1.4.1 Connected Components
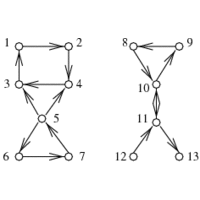
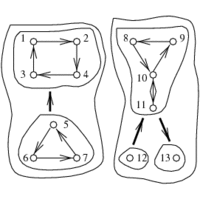
INPUT OUTPUT
Input Description:
A directed or undirected graph G.
A start vertex s.
Problem:
Traverse each edge and vertex of the connected component
containing s.
Excerpt from
The Algorithm Design Manual:
The connected components of a graph represent, in grossest terms, the pieces of the graph. Two vertices are in the
same component of G if and only if there is some path between them.
Finding connected components is at the heart of many graph applications. For example, consider the problem of
identifying clusters in a set of items. We can represent each item by a vertex and add an edge between each pair of
items that are deemed ``similar.'' The connected components of this graph correspond to different classes of items.
Testing whether a graph is connected is an essential preprocessing step for every graph algorithm. Such tests can
be performed so quickly and easily that you should always verify that your input graph is connected, even when you
know it has to be. Subtle, difficult-to-detect bugs often result when your algorithm is run only on one
component of a disconnected graph.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com
Introduction to Algorithms
Introduction to Algorithms
Computer Algorithms
Data Structures and Algorithms
Graph Algorithms
Recreations Mathematiques
