1.4.8 Edge and Vertex Connectivity
INPUT OUTPUT
Input Description:
A graph G.
Optionally, a pair of vertices s and t.
Problem:
What is the smallest subset of vertices (edges) whose deletion
will disconnect G?
Alternately, what is the smallest subset of vertices (edges)
which will separate s from t?
Excerpt from
The Algorithm Design Manual:
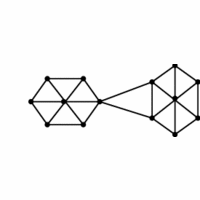
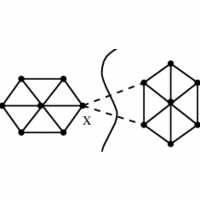
Graph connectivity often arises in problems related to
network reliability. In the context of telephone networks, the vertex connectivity
is the smallest number of switching stations that a terrorist must bomb in order to separate the network, \ie
prevent two unbombed stations from talking to each other.
The edge connectivity is the smallest number of wires that need to be cut to accomplish the same thing. One
well-placed bomb or snipping the right pair of cables suffices to disconnect the network above.
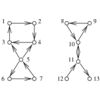
The edge (vertex) connectivity of a graph G is the smallest number
of edge (vertex) deletions sufficient to disconnect G.
There is a close relationship between the two quantities.
The vertex connectivity is always no smaller than the edge connectivity,
since deleting one vertex incident on each edge in a cut set succeeds in
disconnecting the graph. Of course, smaller vertex subsets may be possible.
The minimum vertex degree is an upper bound on both the edge and vertex
connectivity, since deleting all its neighbors (or the edges to all its
neighbors) disconnects the graph into one big and one single-vertex
component.
Recommended Books
Related Problems
This page last modified on 2008-07-10
.
www.algorist.com




 Randomized Algorithms
Randomized Algorithms Network Flows : Theory, Algorithms, and Applications
Network Flows : Theory, Algorithms, and Applications Graph Algorithms
Graph Algorithms